题目内容
已知函数 .
.
(1)当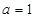 时,指出
时,指出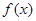 的单调递减区间和奇偶性(不需说明理由);
的单调递减区间和奇偶性(不需说明理由);
(2)当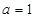 时,求函数
时,求函数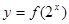 的零点;
的零点;
(3)若对任何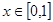 不等式
不等式 恒成立,求实数
恒成立,求实数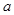 的取值范围。
的取值范围。
【答案】
(1)递减区间为 ,函数
,函数 既不是奇函数也不是偶函数;(2)
既不是奇函数也不是偶函数;(2) 或
或 ;(3)
;(3)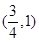 .
.
【解析】
试题分析:(1) 时,作出函数的图象,如下图,即可得出结论.
时,作出函数的图象,如下图,即可得出结论.
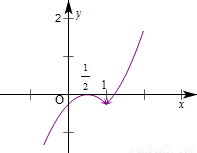
(2)实际上就是解方程 ,只不过在解题时,首先要分类讨论(分
,只不过在解题时,首先要分类讨论(分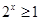 和
和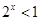 ),其次还要注意的是
),其次还要注意的是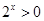 ,否则会得出错误结果;本题也可由求出方程
,否则会得出错误结果;本题也可由求出方程 的正的零点(这可利用(1)的结论很快解决),然后令
的正的零点(这可利用(1)的结论很快解决),然后令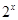 等于这些值,就可求出
等于这些值,就可求出 ;(3)不等式恒成立求参数取值范围问题,一般把问题转化如转化为求函数的值域(或最值)或者利用不等式的性质,本题参数
;(3)不等式恒成立求参数取值范围问题,一般把问题转化如转化为求函数的值域(或最值)或者利用不等式的性质,本题参数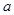 可以分离,在
可以分离,在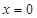 时,不论
时,不论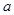 取何值,不等式都成立,在
取何值,不等式都成立,在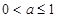 时,可转化为
时,可转化为 ,即
,即 ,下面只要求出
,下面只要求出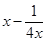 的最大值和
的最大值和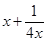 的最小值.
的最小值.
试题解析:1)当 时,函数的单调递减区间为
时,函数的单调递减区间为 (2分)
(2分)
函数 既不是奇函数也不是偶函数(4分)
既不是奇函数也不是偶函数(4分)
(2)当 ,(1分)
,(1分)
由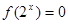 得
得 (2分)
(2分)
即 (4分)
(4分)
解得 (5分)
(5分)
所以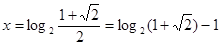 或
或 (6分)
(6分)
(3)当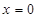 时,
时,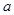 取任意实数,不等式
取任意实数,不等式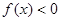 恒成立,
恒成立,
故只需考虑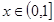 ,此时原不等式变为
,此时原不等式变为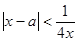 (1分)
(1分)
即
故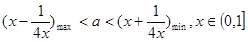 (2分)
(2分)
又函数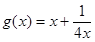 在
在 上单调递增,
上单调递增,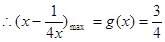 (3分)
(3分)
函数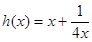 在
在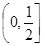 上单调递减,在
上单调递减,在 上单调递增,(4分)
上单调递增,(4分)
 ;(5分)
;(5分)
所以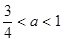 ,即实数
,即实数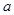 的取值范围是
的取值范围是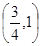 (6分)
(6分)
考点:(1)函数单调区间与奇偶性;(2)解超越方程;(3)不等式恒成立问题.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
 ,
,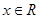 .
.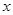 为何值时,
为何值时,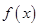 取得最大值,并求出其最大值;
取得最大值,并求出其最大值; ,
,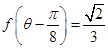 ,求
,求 的值.
的值.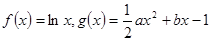 ,
, 且
且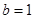 时,证明:对
时,证明:对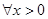 ,
,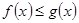 ;
;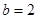 ,且
,且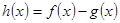 存在单调递减区间,求
存在单调递减区间,求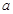 的取值范围;
的取值范围;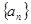 ,若存在常数
,若存在常数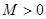 ,
,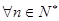 ,都有
,都有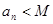 ,则称数列
,则称数列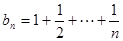 ,试判断数列
,试判断数列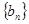 是否有上界.
是否有上界.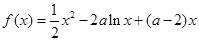 ,
,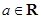 .
.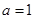 时,求函数
时,求函数 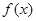 的最小值;
的最小值; 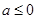 时,讨论函数
时,讨论函数 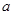 ,对任意的
,对任意的
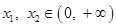 ,且
,且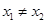 ,有
,有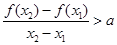 ,恒成立,若存在求出
,恒成立,若存在求出