题目内容
等腰梯形ABCD中,上底CD=1,腰AD=CB=
,下底AB=3,以下底所在直线为x轴,则由斜二测画法画出的直观图A′B′C′D′的面积为 .
| 2 |
分析:根据斜二测画法的规则分别求出等腰梯形的直观图的上底和下底,以及高即可求出面积.
解答: 解:在等腰梯形ABCD中,上底CD=1,腰AD=CB=
解:在等腰梯形ABCD中,上底CD=1,腰AD=CB=
,下底AB=3,
∴高DE=1,
根据斜二测画法的规则可知,A'B'=AB=3,D'C'=DC=1,O'D'=
DE=
,
直观图中的高D'F=O'D'sin45°═
×
=
,
∴直观图A′B′C′D′的面积为
×
=
,
故答案为:
;
 解:在等腰梯形ABCD中,上底CD=1,腰AD=CB=
解:在等腰梯形ABCD中,上底CD=1,腰AD=CB=| 2 |
∴高DE=1,
根据斜二测画法的规则可知,A'B'=AB=3,D'C'=DC=1,O'D'=
| 1 |
| 2 |
| 1 |
| 2 |
直观图中的高D'F=O'D'sin45°═
| 1 |
| 2 |
| ||
| 2 |
| ||
| 4 |
∴直观图A′B′C′D′的面积为
| 1+3 |
| 2 |
| ||
| 4 |
| ||
| 2 |
故答案为:
| ||
| 2 |
点评:本题主要考查斜二测画法的规则,注意平行于坐标轴的直线平行性不变,平行x轴的线段长度不变,平行于y轴的长度减半.

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
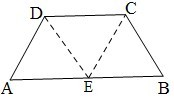 如图,在等腰梯形ABCD中,AB=2DC=2,∠DAB=60°,E为AB的中点,将△ADE与△BEC分别沿ED、EC向上折起,使A、B重合于点P,则P-DCE三棱锥的外接球的体积为( )
如图,在等腰梯形ABCD中,AB=2DC=2,∠DAB=60°,E为AB的中点,将△ADE与△BEC分别沿ED、EC向上折起,使A、B重合于点P,则P-DCE三棱锥的外接球的体积为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
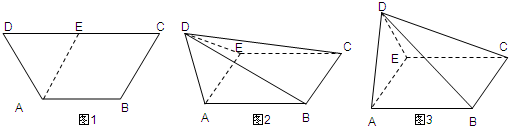 如图1,等腰梯形ABCD中,AB=2,CD=4,∠ADC=∠BCD=60°.取线段CD中点E,将△ADE沿AE折起,如图2所示.
如图1,等腰梯形ABCD中,AB=2,CD=4,∠ADC=∠BCD=60°.取线段CD中点E,将△ADE沿AE折起,如图2所示. 22、如图,在等腰梯形ABCD中,AD∥BC,AB=DC,过点D作AC的平行线DE,交BA的延长线于点E.
22、如图,在等腰梯形ABCD中,AD∥BC,AB=DC,过点D作AC的平行线DE,交BA的延长线于点E. 如图,在等腰梯形ABCD中,M,N分别是AB,CD的中点,沿MN将MNCB折起至MNC1B1,使它与MNDA成直二面角.已知AB=2CD=4MN,给出下列四个等式:
如图,在等腰梯形ABCD中,M,N分别是AB,CD的中点,沿MN将MNCB折起至MNC1B1,使它与MNDA成直二面角.已知AB=2CD=4MN,给出下列四个等式: