题目内容
已知椭圆C1: =1 (a>b>0)与双曲线C2:x2-
=1 (a>b>0)与双曲线C2:x2- =1 有公共的焦点,C2的一条渐近线与以C1的长轴为直径的圆相交于A,B两点.若C1恰好将线段AB三等分,则
=1 有公共的焦点,C2的一条渐近线与以C1的长轴为直径的圆相交于A,B两点.若C1恰好将线段AB三等分,则
- A.a2=

- B.a2=3
- C.b2=

- D.b2=2
C
分析:先由双曲线方程确定一条渐近线方程为y=2x,根据对称性易AB为圆的直径且AB=2a,利用椭圆与双曲线有公共的焦点,得方程a2-b2=5;设C1与y=2x在第一象限的交点的坐标为(x,2x),代入C1的方程得: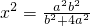 ;对称性知直线y=2x被C1截得的弦长=2
;对称性知直线y=2x被C1截得的弦长=2 x,根据C1恰好将线段AB三等分得:2
x,根据C1恰好将线段AB三等分得:2 x=
x= ,从而可解出a2,b2的值,故可得结论
,从而可解出a2,b2的值,故可得结论
解答:由题意,C2的焦点为(± ,0),一条渐近线方程为y=2x,根据对称性易AB为圆的直径且AB=2a
,0),一条渐近线方程为y=2x,根据对称性易AB为圆的直径且AB=2a
∴C1的半焦距c= ,于是得a2-b2=5 ①
,于是得a2-b2=5 ①
设C1与y=2x在第一象限的交点的坐标为(x,2x),代入C1的方程得: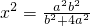 ②,
②,
由对称性知直线y=2x被C1截得的弦长=2 x,
x,
由题得:2 x=
x= ,所以
,所以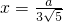 ③
③
由②③得a2=11b2 ④
由①④得a2=5.5,b2=0.5
故选C
点评:本题以椭圆,双曲线为载体,考查直线与圆锥曲线的位置关系,解题思路清晰,但计算有点烦琐,需要小心谨慎.
分析:先由双曲线方程确定一条渐近线方程为y=2x,根据对称性易AB为圆的直径且AB=2a,利用椭圆与双曲线有公共的焦点,得方程a2-b2=5;设C1与y=2x在第一象限的交点的坐标为(x,2x),代入C1的方程得:
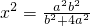 ;对称性知直线y=2x被C1截得的弦长=2
;对称性知直线y=2x被C1截得的弦长=2 x,根据C1恰好将线段AB三等分得:2
x,根据C1恰好将线段AB三等分得:2 x=
x= ,从而可解出a2,b2的值,故可得结论
,从而可解出a2,b2的值,故可得结论解答:由题意,C2的焦点为(±
 ,0),一条渐近线方程为y=2x,根据对称性易AB为圆的直径且AB=2a
,0),一条渐近线方程为y=2x,根据对称性易AB为圆的直径且AB=2a∴C1的半焦距c=
 ,于是得a2-b2=5 ①
,于是得a2-b2=5 ①设C1与y=2x在第一象限的交点的坐标为(x,2x),代入C1的方程得:
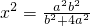 ②,
②,由对称性知直线y=2x被C1截得的弦长=2
 x,
x,由题得:2
 x=
x= ,所以
,所以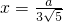 ③
③由②③得a2=11b2 ④
由①④得a2=5.5,b2=0.5
故选C
点评:本题以椭圆,双曲线为载体,考查直线与圆锥曲线的位置关系,解题思路清晰,但计算有点烦琐,需要小心谨慎.

练习册系列答案
相关题目
 =1 (a>b>0)与双曲线C2:x2-
=1 (a>b>0)与双曲线C2:x2-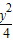 =1 有公共的焦点,C2的一条渐近线与以C1的长轴为直径的圆相交于A,B两点.若C1恰好将线段AB三等分,则( )
=1 有公共的焦点,C2的一条渐近线与以C1的长轴为直径的圆相交于A,B两点.若C1恰好将线段AB三等分,则( )

 +
+ =1(a>b>0)的长轴长为4,离心率为
=1(a>b>0)的长轴长为4,离心率为 ,F1、F2分别为其左右焦点.一动圆过点F2,且与直线x=-1相切.
,F1、F2分别为其左右焦点.一动圆过点F2,且与直线x=-1相切. 共线,
共线, 与
与 共线,且
共线,且 •
• =0,求四边形PMQN面积的最小值.
=0,求四边形PMQN面积的最小值. =1(a>b>0)的左、右焦点分别为F1、F2,其中F2也是抛物线C2:y2=4x的焦点,M是C1与C2在第一象限的交点,且
=1(a>b>0)的左、右焦点分别为F1、F2,其中F2也是抛物线C2:y2=4x的焦点,M是C1与C2在第一象限的交点,且
 +
+ =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ,直线l:x-y+
,直线l:x-y+ =0与椭圆C1相切.
=0与椭圆C1相切.