题目内容
已知椭圆C1：
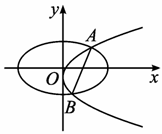
=1,抛物线C2：(y-m)2=2px(p＞0),且C1、C2的公共弦AB过椭圆C1的右焦点.(1)当AB⊥x轴时，求m、p的值，并判断抛物线C2的焦点是否在直线AB上；
(2)若p=
且抛物线C2的焦点在直线AB上，求m的值及直线AB的方程.
解：（1）当AB⊥x轴时，点A、B关于x轴对称.
所以m=0，直线AB的方程为x=1，从而点A的坐标为（1，）或（1，-）.
因为点A在抛物线上，所以
=2p,即p=
.
此时C2的焦点坐标为（
，0），该焦点不在直线AB上.
（2）当C2的焦点在AB上时，由（1）知直线AB的斜率存在，设直线AB的方程为y=k(x-1).
由
消去y得（3+4k2）x2-8k2x+4k2-12=0 ①
设A、B的坐标分别为（x1,y1）(x2,y2),
则x1、x2是方程①的两根，x1+x2=
.
因为AB既是过C1的右焦点的弦，又是过C2的焦点的弦，
所以|AB|=（2-
x1）+(2-
x2)=4-
(x1+x2),
且|AB|=（x1+
）+(x2+
)=x1+x2+p=x1+x2+
.
从而x1+x2+
=4-
(x1+x2).
所以x1+x2=
,即
解得k2=6,即k=±
.
因为C2的焦点F′(
,m)在直线y=k(x-1)上，
所以m=-
k,即m=
或m=-
.
当m=
时，直线AB的方程为y=-
(x-1);
当m=-
时，直线AB的方程为y=
(x-1).
练习册系列答案
相关题目
=1 （a＞b＞0）与双曲线C2：x2-
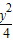=1 有公共的焦点，C2的一条渐近线与以C1的长轴为直径的圆相交于A，B两点．若C1恰好将线段AB三等分，则（ ）
+
=1（a＞b＞0）的长轴长为4，离心率为
，F1、F2分别为其左右焦点．一动圆过点F2，且与直线x=-1相切．
共线，
与
共线，且
•
=0，求四边形PMQN面积的最小值．
=1（a＞b＞0）的左、右焦点分别为F1、F2，其中F2也是抛物线C2：y2=4x的焦点，M是C1与C2在第一象限的交点，且
+
=1（a＞b＞0）的离心率为
，直线l：x-y+
=0与椭圆C1相切．