题目内容
已知向量 =(cos
=(cos ,sin
,sin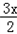 ),
),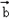 =(cos
=(cos ,﹣sin
,﹣sin ),
), =(
=( ,﹣1),其中x⊥R.
,﹣1),其中x⊥R.
(1)当 ⊥
⊥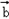 时,求x值的集合;
时,求x值的集合;
(2)求| ﹣
﹣ |的最大值.
|的最大值.
 =(cos
=(cos ,sin
,sin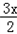 ),
),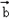 =(cos
=(cos ,﹣sin
,﹣sin ),
), =(
=( ,﹣1),其中x⊥R.
,﹣1),其中x⊥R.(1)当
 ⊥
⊥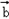 时,求x值的集合;
时,求x值的集合;(2)求|
 ﹣
﹣ |的最大值.
|的最大值.解:(1)由 ⊥
⊥

 =0,
=0,
即cos cos
cos ﹣sin
﹣sin sin
sin =0,
=0,
得cos2x=0,
则2x=kπ+ (k∈Z),
(k∈Z),
∴x= (k∈Z),
(k∈Z),
∴当 ⊥
⊥ 时,x值的集合为{x|x=
时,x值的集合为{x|x= (k∈Z)};
(k∈Z)};
(2)| ﹣
﹣ |2=(
|2=( )2=
)2= 2﹣2
2﹣2 +
+ 2=|
2=| |2﹣2
|2﹣2 +|
+| |2,
|2,
又| |2=(cos
|2=(cos )2+(sin
)2+(sin )2=1,
)2=1,
| |2=(
|2=( )2+(﹣1)2=4,
)2+(﹣1)2=4,
 =
= cos
cos ﹣sin
﹣sin =2(
=2( cos
cos ﹣
﹣ sin
sin )=2cos(
)=2cos( +
+ ),
),
∴| |2=1﹣4cos(
|2=1﹣4cos( +
+ )+4=5﹣4cos(
)+4=5﹣4cos( +
+ ),
),
∴| |2max=9,
|2max=9,
∴| |max=3,即|
|max=3,即| |的最大值为3.
|的最大值为3.
 ⊥
⊥

 =0,
=0,即cos
 cos
cos ﹣sin
﹣sin sin
sin =0,
=0,得cos2x=0,
则2x=kπ+
 (k∈Z),
(k∈Z),∴x=
 (k∈Z),
(k∈Z),∴当
 ⊥
⊥ 时,x值的集合为{x|x=
时,x值的集合为{x|x= (k∈Z)};
(k∈Z)};(2)|
 ﹣
﹣ |2=(
|2=( )2=
)2= 2﹣2
2﹣2 +
+ 2=|
2=| |2﹣2
|2﹣2 +|
+| |2,
|2,又|
 |2=(cos
|2=(cos )2+(sin
)2+(sin )2=1,
)2=1,|
 |2=(
|2=( )2+(﹣1)2=4,
)2+(﹣1)2=4, =
= cos
cos ﹣sin
﹣sin =2(
=2( cos
cos ﹣
﹣ sin
sin )=2cos(
)=2cos( +
+ ),
),∴|
 |2=1﹣4cos(
|2=1﹣4cos( +
+ )+4=5﹣4cos(
)+4=5﹣4cos( +
+ ),
),∴|
 |2max=9,
|2max=9,∴|
 |max=3,即|
|max=3,即| |的最大值为3.
|的最大值为3.
练习册系列答案
相关题目
已知向量
=(cosα,sinα),
=(cosβ,sinβ),若|
-
|=
,则
和
的夹角为( )
| a |
| b |
| a |
| b |
| 2 |
| a |
| b |
| A、60° | B、90° |
| C、120° | D、150° |