题目内容
(1)设m等于|a|、|b|和1中最大的一个,当|x|>m时,求证:| +
+ |<2;
|<2;
(2)已知a、b∈R,且a≠0,求证 ≥|a|-|b|.
≥|a|-|b|.
答案:
解析:
解析:
|
(1)因为|x|>m≥|a|,|x|>m≥|b|,|x|>m≥1,所以|x|2>|b|,所以 | 故原不等式成立. (2)当|a|≤|b|时,左边≥0,右边≤0,所以不等式成立;当|a|>|b|时,|
综上知,原不等式成立. |

练习册系列答案
相关题目
 +
+ |≤|
|≤| |+|
|+| +
+ <
< +
+ =2
=2 |<1,则
|<1,则 =|a-
=|a- |≥|a|-|
|≥|a|-| |>|a|-|b|
|>|a|-|b|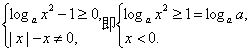 ,a>1},则
,a>1},则