题目内容
若函数f(x)=ax(a>0,a≠1)为增函数,那么g(x)=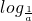
 的图象是
的图象是
- A.

- B.

- C.

- D.

C
分析:要想判断函数g(x)=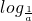
 的图象,我们可以先观察到函数的解析式中x的取值范围,得到其定义域从而得到图象的大致位置,再根据基本初等函数的性质,对其进行分析,找出符合函数性质的图象即可.
的图象,我们可以先观察到函数的解析式中x的取值范围,得到其定义域从而得到图象的大致位置,再根据基本初等函数的性质,对其进行分析,找出符合函数性质的图象即可.
解答:∵函数f(x)=ax(a>0,a≠1)为增函数,
∴a>1,?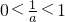 ,
,
考察函数g(x)=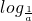
 的定义域:由
的定义域:由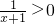 得x>-1,
得x>-1,
则函数的定义域为:(-1,+∞),即函数图象只出现在直线x=-1轴右侧;
又函数g(x)=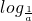
 可看成g(x)=
可看成g(x)=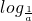 u,u=
u,u= 的复合,
的复合,
其中g(x)=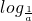 u和u=
u和u= 均在各自的定义域是减函数,
均在各自的定义域是减函数,
从而得出函数g(x)=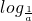
 在区间(-1,+∞)上递增,
在区间(-1,+∞)上递增,
且当x=0时,g(0)=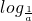
 =0,即图象过原点,
=0,即图象过原点,
分析A、B、C、D四个答案,只有C满足要求.
故选C.
点评:要想判断函数的图象,我们先要求出其定义域,再根据解析式,分析其单调性、奇偶性、周期性等性质,根据定义域、值域分析函数图象所处的区域,根据函数的性质分析函数图象的形状,如果还不能判断的话,可以代入特殊值,根据特殊点的位置进行判断.
分析:要想判断函数g(x)=
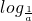
 的图象,我们可以先观察到函数的解析式中x的取值范围,得到其定义域从而得到图象的大致位置,再根据基本初等函数的性质,对其进行分析,找出符合函数性质的图象即可.
的图象,我们可以先观察到函数的解析式中x的取值范围,得到其定义域从而得到图象的大致位置,再根据基本初等函数的性质,对其进行分析,找出符合函数性质的图象即可.解答:∵函数f(x)=ax(a>0,a≠1)为增函数,
∴a>1,?
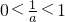 ,
,考察函数g(x)=
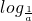
 的定义域:由
的定义域:由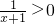 得x>-1,
得x>-1,则函数的定义域为:(-1,+∞),即函数图象只出现在直线x=-1轴右侧;
又函数g(x)=
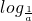
 可看成g(x)=
可看成g(x)=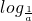 u,u=
u,u= 的复合,
的复合,其中g(x)=
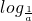 u和u=
u和u= 均在各自的定义域是减函数,
均在各自的定义域是减函数,从而得出函数g(x)=
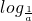
 在区间(-1,+∞)上递增,
在区间(-1,+∞)上递增,且当x=0时,g(0)=
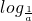
 =0,即图象过原点,
=0,即图象过原点,分析A、B、C、D四个答案,只有C满足要求.
故选C.
点评:要想判断函数的图象,我们先要求出其定义域,再根据解析式,分析其单调性、奇偶性、周期性等性质,根据定义域、值域分析函数图象所处的区域,根据函数的性质分析函数图象的形状,如果还不能判断的话,可以代入特殊值,根据特殊点的位置进行判断.

练习册系列答案
相关题目