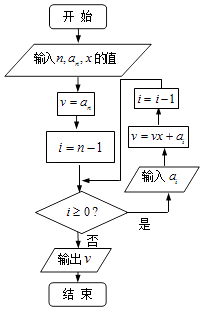
题目内容
【题目】在等比数列{an}中，公比q＞1，且满足a2+a3+a4=28，a3+2是a2与a4的等差中项．
（1）求数列{an}的通项公式；
（2）若bn=log2an+5 ， 且数列{bn}的前n项的和为Sn ， 求数列{ 
}的前n项和Tn ．
【答案】
（1）解：∵a2+a3+a4=28，∴a1q+a1q2+a1q3=28①；又a3+2是a2、a4的等差中项得到2（a1q2+2）=a1q+a1q3②．
由①得：a1q（1+q+q2）=28③，由②得：a1q2=8，a1q+a1q3=20即a1q（1+q2）=20④
③÷④得 
∴2q2﹣5q+2=0
∴q=2或q= 
∵q＞1，∴q=2
∴数列{an}的通项公式an=a3qn﹣3=2n；
（2）解：∵an=2n，∴bn=log2 
=n+5，∴b1=6
∴数列{bn}是以6为首项，1为公差的等差数列，
∴Sn= 
∴ 
= 
∴数列{ }是以6为首项， 为公差的等差数列，
∴Tn= 
= 
．
【解析】（1）利用a2+a3+a4=28，a3+2是a2与a4的等差中项，建立方程，求出数列的公比，即可求数列{an}的通项公式；（2）确定数列{bn}的通项及前n的和，求得数列{ }的通项，即可求和．
【考点精析】认真审题，首先需要了解数列的前n项和(数列{an}的前n项和sn与通项an的关系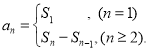
)．
练习册系列答案
相关题目
