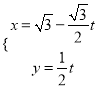题目内容
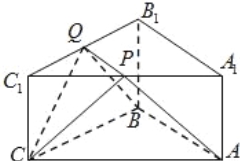
【题目】如图,ABC﹣A1B1C1是底面边长为2,高为![]() 的正三棱柱,经过AB的截面与上底面相交于PQ,设C1P=λC1A1(0<λ<1).
的正三棱柱,经过AB的截面与上底面相交于PQ,设C1P=λC1A1(0<λ<1).

(Ⅰ)证明:PQ∥A1B1;
(Ⅱ)当![]() 时,在图中作出点C在平面ABQP内的正投影F(说明作法及理由),并求四面体CABF的体积.
时,在图中作出点C在平面ABQP内的正投影F(说明作法及理由),并求四面体CABF的体积.
【答案】(Ⅰ)证明见解析;(Ⅱ)正投影见解析,![]() .
.
【解析】
试题分析:(I)由正三棱柱的性质可以知道,上下两个底面平行,由两个平面平行的性质定理可得![]() ,由此能证明
,由此能证明![]() ;(II) 当
;(II) 当![]() 时,
时,![]() 分别是
分别是![]() 的中点, 在等腰梯形
的中点, 在等腰梯形![]() 中,
中,![]() ,
,![]() 平面
平面![]() ,即
,即![]() ,所以
,所以![]() 点是
点是![]() 在平面
在平面![]() 内的正投影,即得.
内的正投影,即得.
试题解析:(I)∵平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() ,,又
,,又![]() .
.
(Ⅱ)![]() 点是
点是![]() 中点,理由如下:
中点,理由如下:
当![]() 时,
时,![]() 分别是
分别是![]() 的中点,连接
的中点,连接![]() 和
和![]() , 因为
, 因为![]()
是正三棱柱,所以![]() ,
,
取![]() 中点
中点![]() ,连接
,连接![]() 在等腰梯形
在等腰梯形![]() 中,
中,![]() ,
,
连接![]() 中,
中,![]()
![]()
![]() ,
,
![]() 平面ABF,即
平面ABF,即![]() ,
,
所以![]() 点是
点是![]() 在平面
在平面![]() 内的正投影。
内的正投影。
![]()

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目