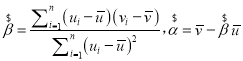题目内容
【题目】如图,三棱柱![]() 中,
中,![]() ,
,![]() 为四边形
为四边形![]() 对角线交点,
对角线交点,![]() 为棱
为棱![]() 的中点,且
的中点,且![]() 平面
平面![]() .
.
(1)证明:![]() 平面
平面![]() ;
;
(2)证明:四边形![]() 为矩形.
为矩形.
【答案】(1)见解析(2)见解析
【解析】
(1)取![]() 中点
中点![]() ,连结
,连结![]() ,由题意
,由题意![]() 且
且![]() ,证出
,证出![]() ,且
,且![]() ,进而可得
,进而可得![]() ,利用线面平行的判定定理即可证出.
,利用线面平行的判定定理即可证出.
(2)首先证出![]() ,利用线面垂直的性质定理证出
,利用线面垂直的性质定理证出![]() ,再利用线面垂直的判定定理证出
,再利用线面垂直的判定定理证出![]() 平面
平面![]() ,从而可证出
,从而可证出![]() ,根据
,根据![]() ,即证
,即证![]() .
.
证明:(1)取![]() 中点
中点![]() ,连结
,连结![]() .
.

在三棱柱![]() 中,四边形
中,四边形![]() 为平行四边形,
为平行四边形,
![]() 且
且![]() .
.
因为![]() 为平行四边形
为平行四边形![]() 对角线的交点,所以
对角线的交点,所以![]() 为
为![]() 中点,
中点,
又![]() 为
为![]() 中点,所以
中点,所以![]() ,且
,且![]() .
.
又![]() ,
,![]() ,所以
,所以![]() ,且
,且![]() .
.
又![]() 为
为![]() 中点,所以
中点,所以![]() ,且
,且![]() ,
,
所以![]() 为平行四边形,
为平行四边形,
所以![]() ,
,
又因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() :
:
(2)因为![]() ,
,![]() 为
为![]() 中点,所以
中点,所以![]() ,
,
又因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() .
.
因为![]() ,
,![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,
所以![]() 平面
平面![]() .
.
又![]() 平面
平面![]() ,所以
,所以![]() ,
,
又由(1)知![]() ,所以
,所以![]() ,
,
在三棱柱![]() 中,四边形
中,四边形![]() 为平行四边形,
为平行四边形,
所以四边形![]() 为矩形.
为矩形.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
【题目】为了研究某学科成绩是否与学生性别有关,采用分层抽样的方法,从高三年级抽取了30名男生和20名女生的该学科成绩,得到如下所示男生成绩的频率分布直方图和女生成绩的茎叶图,规定80分以上为优分(含80分).

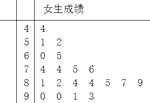
(Ⅰ)(i)请根据图示,将2×2列联表补充完整;
优分 | 非优分 | 总计 | |
男生 | |||
女生 | |||
总计 | 50 |
(ii)据此列联表判断,能否在犯错误概率不超过10%的前提下认为“该学科成绩与性别有关”?
(Ⅱ)将频率视作概率,从高三年级该学科成绩中任意抽取3名学生的成绩,求至少2名学生的成绩为优分的概率.
附:
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
![]() .
.