题目内容
当n∈N*时,试比较an=2n与bn=n2的大小.
解析:a1=2,b1=1,∴a1>b1;?
a2=4,b2=4,∴a2=b2;?
a3=8,b3=9,∴a3<b3;?
a4=16,b4=16,∴a4=b4;?
a5=32,b5=25,∴a5>b5;?
a6=64,b6=36,∴a6>b6.?
猜想:n≥5时,an>bn(以下用数学归纳法证明当n≥5时,an>bn).?
(1)当n=5时,a5=32,b5=25,a5>b5成立.?
(2)假设当n=k(k∈N*,k≥5)时,有ak>bk,即2k>k2(k≥5),?
因此ak+1-bk+1=2k+1-(k+1)2=2·2k-(k2+2k+1)>2k2-(k2+2k+1)?
=k2-2k-1=(k-1)2-2.?
∵k≥5,∴(k-1)2≥16.?
∴(k-1)2-2>0,即ak+1>bk+1?.?
这表明当n=k+1时,ak+1>bk+1.?
根据(1)(2)可知,当n≥5(n∈N*)时an>bn.?
综上可知,当n=2,4时,an=bn;当n=3时,an<bn;当n=1或n≥5时,an>bn.

练习册系列答案
相关题目
 。
。 在定义域上是奇函数;
在定义域上是奇函数;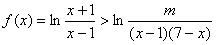 恒成立,求实数m的取值范围;
恒成立,求实数m的取值范围;
 在定义域上是奇函数;
在定义域上是奇函数; 恒成立,求实数m的取值范围;
恒成立,求实数m的取值范围;
 在定义域上是奇函数;
在定义域上是奇函数; 恒成立,求实数m的取值范围;
恒成立,求实数m的取值范围;
 在定义域上是奇函数;
在定义域上是奇函数; 恒成立,求实数m的取值范围;
恒成立,求实数m的取值范围;