题目内容
已知直线x过双曲线
-
=1(a>0,b>0)右焦点,交双曲线于A,B两点,若
的最小值为2,则其离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
| |AB| |
| 2a |
分析:利用双曲线的性质可求得
=2,从而可求得其离心率.
| b2 |
| a2 |
解答:解:∵直线x过
-
=1(a>0,b>0)的右焦点,交双曲线于A,B两点,
当且仅当过右焦点的直线与x轴垂直时,
最小,
又当过右焦点的直线AB与x轴垂直时,设A(c,y0),
则
-
=1,
∴|y0|=
,
∴|AB|=2×
,
∵
的最小值为2,
∴
=2,又a2+b2=c2,
∴
=
=3,
即离心率e2=3,
∴e=
.
故选B.
| x2 |
| a2 |
| y2 |
| b2 |
当且仅当过右焦点的直线与x轴垂直时,
| |AB| |
| 2a |
又当过右焦点的直线AB与x轴垂直时,设A(c,y0),
则
| c2 |
| a2 |
| y02 |
| b2 |
∴|y0|=
| b2 |
| a |
∴|AB|=2×
| b2 |
| a |
∵
| |AB| |
| 2a |
∴
| b2 |
| a2 |
∴
| b2+a2 |
| a2 |
| c2 |
| a2 |
即离心率e2=3,
∴e=
| 3 |
故选B.
点评:本题考查双曲线的简单性质,由
的最小值为2,求得
=2是关键,考查分析、理解与应用双曲线的简单性质的能力,属于中档题.
| |AB| |
| 2a |
| b2 |
| a2 |

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
 (a>0,b>0)右焦点,交双曲线于A,B两点,若
(a>0,b>0)右焦点,交双曲线于A,B两点,若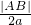 的最小值为2,则其离心率为
的最小值为2,则其离心率为
