Question

【题目】已知函数 在点 处的切线方程是 .

（1）求 ， 的值及函数 的最大值；

（2）若实数 ， 满足 （ ）

1）证明： ；

2）若 ，证明： .

Answer 1

【答案】(1)时，．(2)(i)见解析;(ii)见解析.

【解析】分析：（Ⅰ）求出，由可得确定函数的解析式，分别令求得的范围，可得函数增区间，求得的范围，可得函数的减区间；（Ⅱ）（ⅰ）结合（Ⅰ），可得，即.

又因为，所以，故；（ⅱ）由

可得，令，利用导数研究函数的单调性，可得，从而得，，进而可得结果.

详解：（Ⅰ），

由题意有，解得．

故，，

，所以在为增函数，在为减函数．

故有当时，．

（Ⅱ）证明：

（ⅰ），

由（Ⅰ）知，所以，即.

又因为，所以，故.

（ⅱ）法一：

由（1）知

在上单调递增

即：

法二：，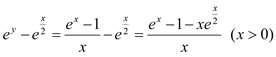

构造函数，，

因为，所以，

即当时，，所以在为增函数，

所以，即，故