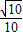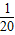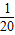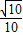题目内容
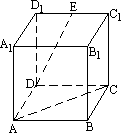
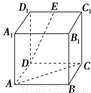
在如图所示的正方体ABCD—A1B(1)求AE与D
(2)证明平面AED⊥平面A1FD1.
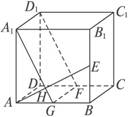
解法一:(1)解:∵AC1是正方体,

∴AD⊥面DC1.
又D1F![]() 面DC1,∴AD⊥D
面DC1,∴AD⊥D
取AB的中点G,连结A
∵F是CD的中点,∴GF、AD平行且相等,
即GF![]() AD.
AD.
又A1D1![]() AD,∴GF
AD,∴GF![]() A1D1.
A1D1.
故GFD
设A
∵E是BB1的中点,∴Rt△A1AG≌Rt△ABE.
∴∠GA
从而∠AHA1=90°,即直线AE与D
(2)证明:由(1)知,AD⊥D
又AD∩AE=A,∴D
又∵D1F![]() 平面A1FD1,∴面AED⊥面A1FD1.
平面A1FD1,∴面AED⊥面A1FD1.
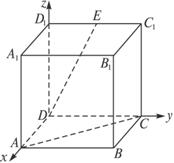
解法二:(1)解:如图所示建立空间坐标系,D为坐标原点.
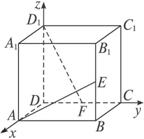
设DC=a,依题意有
D(0,0,0),A(a,0,0),D1(0,0,a),F(0, ![]() ,0).
,0).
![]() =(0,
=(0, ![]() ,-a),E(a,a,
,-a),E(a,a, ![]() ),
),![]() =(0,a,
=(0,a, ![]() ).
).
![]() ·
·![]() =0+a·
=0+a·![]() +(-a)·
+(-a)·![]() =0,
=0,
∴AE、D
(2)证明:同证法一.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
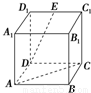
 在如图所示的正方体A1B1C1D1ABCD中,E是C1D1的中点,则异面直线DE与AC夹角的余弦值为( )
在如图所示的正方体A1B1C1D1ABCD中,E是C1D1的中点,则异面直线DE与AC夹角的余弦值为( )