题目内容
不等式
>t+l(t<0)解集是( )
| x |
| x-1 |
A、{x|x>1或x<1+
| ||
B、{x|1<x<1+
| ||
C、{x|1+
| ||
D、{x|x>1+
|
分析:将原不等式移项、同分,根据两个数的商是正数则它们的积是正数,将原不等式同解变形为一元二次不等式,通过解二次不等式求出解集.
解答:解:
>t+l(t<0)同解于
>0同解于
[-tx-(t+1)](x-1)>0
∴x>1或x<1+
∴不等式的解集为{x|x>1或x<1+
}
故选A
| x |
| x-1 |
| -tx-(t+1) |
| x-1 |
[-tx-(t+1)](x-1)>0
∴x>1或x<1+
| 1 |
| t |
∴不等式的解集为{x|x>1或x<1+
| 1 |
| t |
故选A
点评:求分式不等式、无理不等式时,一般是通过同解变形转化为一元一次不等式或一元二次不等式解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
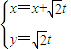 (t为参数).若圆C被直线l平分,则实数x的值为 .
(t为参数).若圆C被直线l平分,则实数x的值为 .