题目内容
若椭圆的对称轴为坐标轴,长轴长与短轴长的和为18,焦距为6,则椭圆的方程为
- A.

- B.

- C.
 或
或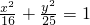
- D.以上都不对
C
分析:设出椭圆的长半轴与短半轴分别为a和b,根据长轴与短轴的和为18列出关于a与b的方程记作①,由焦距等于6求出c的值,根据椭圆的基本性质a2-b2=c2,把c的值代入即可得到关于a与b的另一关系式记作②,将①②联立即可求出a和b的值,然后利用a与b的值写出椭圆的方程即可.
解答:设椭圆的长半轴与短半轴分别为a和b,
则2(a+b)=18,即a+b=9①,
由焦距为6,得到c=3,则a2-b2=c2=9②,
由①得到a=9-b③,把③代入②得:
(9-b)2-b2=9,化简得:81-18b=9,解得b=4,把b=4代入①,解得a=5,
所以椭圆的方程为: +
+ =1或
=1或  +
+ =1.
=1.
故选C.
点评:此题考查学生掌握椭圆的基本性质,会根据椭圆的长半轴与短半轴写出椭圆的标准方程,是一道综合题.学生做题时应注意焦点在x轴和y轴上两种情况.
分析:设出椭圆的长半轴与短半轴分别为a和b,根据长轴与短轴的和为18列出关于a与b的方程记作①,由焦距等于6求出c的值,根据椭圆的基本性质a2-b2=c2,把c的值代入即可得到关于a与b的另一关系式记作②,将①②联立即可求出a和b的值,然后利用a与b的值写出椭圆的方程即可.
解答:设椭圆的长半轴与短半轴分别为a和b,
则2(a+b)=18,即a+b=9①,
由焦距为6,得到c=3,则a2-b2=c2=9②,
由①得到a=9-b③,把③代入②得:
(9-b)2-b2=9,化简得:81-18b=9,解得b=4,把b=4代入①,解得a=5,
所以椭圆的方程为:
 +
+ =1或
=1或  +
+ =1.
=1.故选C.
点评:此题考查学生掌握椭圆的基本性质,会根据椭圆的长半轴与短半轴写出椭圆的标准方程,是一道综合题.学生做题时应注意焦点在x轴和y轴上两种情况.

练习册系列答案
相关题目
若椭圆的对称轴为坐标轴,长轴长与短轴长的和为18,一个焦点的坐标是(3,0),则椭圆的标准方程为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 ,一个焦点的坐标是(3,0),则椭圆的标准方程为( )
,一个焦点的坐标是(3,0),则椭圆的标准方程为( ) B.
B.
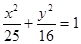 C.
C.  D.
D.

 :
: 可把平面直角坐标系上的一点
可把平面直角坐标系上的一点 变换到这一平面上的一点
变换到这一平面上的一点 .
. 的中心为坐标原点,焦点在
的中心为坐标原点,焦点在 轴上,且焦距为
轴上,且焦距为 ,长轴顶点和短轴顶点间的距离为2. 求该椭圆
,长轴顶点和短轴顶点间的距离为2. 求该椭圆 、
、 经变换公式
经变换公式 和
和 的坐标;
的坐标; 上一点
上一点 经变换公式
经变换公式 与点
与点 B.
B.  C.
C.  D.
D. 