题目内容
已知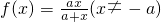 ,且f(2)=1.
,且f(2)=1.
(Ⅰ)求a的值;
(Ⅱ)若在数列{an}中,a1=1,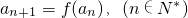 ,计算a2,a3,a4,并由此猜想通项公式an;
,计算a2,a3,a4,并由此猜想通项公式an;
(Ⅲ)证明(Ⅱ)中的猜想.
解:(Ⅰ)因为 ,f(2)=1,
,f(2)=1,
所以 =1,解得 a=2. …(2分)
=1,解得 a=2. …(2分)
(Ⅱ)在{an}中,因为a1=1, .
.
所以 ,
, ,
, ,
,
所以猜想{an}的通项公式为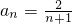 .…(6分)
.…(6分)
(Ⅲ)证明:因为a1=1,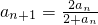 ,
,
所以 ,即
,即 .
.
所以 是以
是以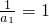 为首项,公差为
为首项,公差为 的等差数列.
的等差数列.
所以 ,所以通项公式
,所以通项公式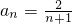 .…(9分)
.…(9分)
分析:(Ⅰ)因为 ,f(2)=1,可得
,f(2)=1,可得 =1,由此解得a的值.
=1,由此解得a的值.
(Ⅱ)根据在{an}中,a1=1, ,令n=1、2、3,即可求得a2,a3,a4的值,由此猜想通项公式an.
,令n=1、2、3,即可求得a2,a3,a4的值,由此猜想通项公式an.
(Ⅲ)由题意可得 ,即
,即 ,根据等差数列的通项公式求出
,根据等差数列的通项公式求出 的通项公式,即可得到{an}的通项公式.
的通项公式,即可得到{an}的通项公式.
点评:本题主要考查用待定系数法求函数的解析式,不完全归纳法的应用,用综合法证明等式,式子的变形是解题的关键,属于中档题.
 ,f(2)=1,
,f(2)=1,所以
 =1,解得 a=2. …(2分)
=1,解得 a=2. …(2分)(Ⅱ)在{an}中,因为a1=1,
 .
.所以
 ,
, ,
, ,
,所以猜想{an}的通项公式为
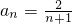 .…(6分)
.…(6分)(Ⅲ)证明:因为a1=1,
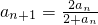 ,
,所以
 ,即
,即 .
.所以
 是以
是以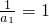 为首项,公差为
为首项,公差为 的等差数列.
的等差数列.所以
 ,所以通项公式
,所以通项公式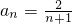 .…(9分)
.…(9分)分析:(Ⅰ)因为
 ,f(2)=1,可得
,f(2)=1,可得 =1,由此解得a的值.
=1,由此解得a的值.(Ⅱ)根据在{an}中,a1=1,
 ,令n=1、2、3,即可求得a2,a3,a4的值,由此猜想通项公式an.
,令n=1、2、3,即可求得a2,a3,a4的值,由此猜想通项公式an.(Ⅲ)由题意可得
 ,即
,即 ,根据等差数列的通项公式求出
,根据等差数列的通项公式求出 的通项公式,即可得到{an}的通项公式.
的通项公式,即可得到{an}的通项公式.点评:本题主要考查用待定系数法求函数的解析式,不完全归纳法的应用,用综合法证明等式,式子的变形是解题的关键,属于中档题.

练习册系列答案
相关题目
 ,且f(2)=1.
,且f(2)=1. ,计算a2,a3,a4,并由此猜想通项公式an;
,计算a2,a3,a4,并由此猜想通项公式an;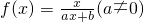 满足f(2)=1,且方程f(x)=x有且仅有一个实数根.
满足f(2)=1,且方程f(x)=x有且仅有一个实数根.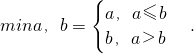 对于(Ⅱ)中的数列{an},令
对于(Ⅱ)中的数列{an},令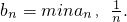 设Sn为数列{bn}的前n项和,求证:Sn>ln(n+1).
设Sn为数列{bn}的前n项和,求证:Sn>ln(n+1).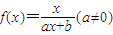 满足f(2)=1,且方程f(x)=x有且仅有一个实数根.
满足f(2)=1,且方程f(x)=x有且仅有一个实数根.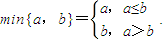 对于(Ⅱ)中的数列{an},令
对于(Ⅱ)中的数列{an},令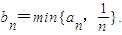 设Sn为数列{bn}的前n项和,求证:Sn>ln(n+1).
设Sn为数列{bn}的前n项和,求证:Sn>ln(n+1).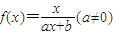 满足f(2)=1,且方程f(x)=x有且仅有一个实数根.
满足f(2)=1,且方程f(x)=x有且仅有一个实数根.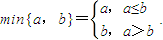 对于(Ⅱ)中的数列{an},令
对于(Ⅱ)中的数列{an},令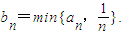 设Sn为数列{bn}的前n项和,求证:Sn>ln(n+1).
设Sn为数列{bn}的前n项和,求证:Sn>ln(n+1).