题目内容
已知函数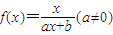 满足f(2)=1,且方程f(x)=x有且仅有一个实数根.
满足f(2)=1,且方程f(x)=x有且仅有一个实数根.(Ⅰ)求函数f(x)的解析式;
(Ⅱ)设数列{an}满足a1=1,an+1=f(an)≠1,n∈N*.求数列{an}的通项公式;
(Ⅲ)定义
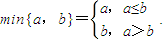 对于(Ⅱ)中的数列{an},令
对于(Ⅱ)中的数列{an},令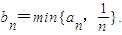 设Sn为数列{bn}的前n项和,求证:Sn>ln(n+1).
设Sn为数列{bn}的前n项和,求证:Sn>ln(n+1).
【答案】分析:(Ⅰ)由题设条件知2a+b=2.当△=(b-1)2=0时,b=1, ,
, ;当△=(b-1)2≠0时,a=1,f(x)=1(x≠0).
;当△=(b-1)2≠0时,a=1,f(x)=1(x≠0).
(Ⅱ)由题意知当f(x)=1时,an+1=1,不合题意,所以 ,
, ,∴
,∴ ,由此可得数列{an}的通项公式.
,由此可得数列{an}的通项公式.
(Ⅲ)由题设条件知, ,所以
,所以 ,
, ,再用分析法证明Sn>ln(n+1).
,再用分析法证明Sn>ln(n+1).
解答:解:(Ⅰ)由 ,得2a+b=2;
,得2a+b=2;
又 ,有且仅有一个解,
,有且仅有一个解,
即ax2+(b-1)x=0,有唯一解满足ax+b≠0.
∵a≠0,∴当△=(b-1)2=0时,b=1,x=0,则 ,此时
,此时 ,
,
又当△=(b-1)2≠0时, ,因为ax1+b=1≠0,
,因为ax1+b=1≠0,
所以ax2+b=b=0,则a=1,此时
综上所述, ,或者f(x)=1(x≠0);
,或者f(x)=1(x≠0);
(Ⅱ)a1=1,an+1=f(an)≠1,n∈N*,当f(x)=1时,an+1=1,不合题意,
则 ,
, ,
,
∴ ,
,
则 ,
,
(Ⅲ)由(Ⅱ)知,
∴ ,则
,则 ,所以
,所以
设数列{cn}的前n项和为Tn=ln(n+1),则c1=T1=ln2<lne=1
当n≥2时, ,要证明
,要证明
令 ,只要证明:lnt<t-1,其中t>1.
,只要证明:lnt<t-1,其中t>1.
令g(x)=x-1-lnx(x≥1),则 ,所以g(x)在[1,+∞)上是增函数,
,所以g(x)在[1,+∞)上是增函数,
则当x>1时,g(x)>g(1)=0,即x-1>lnx(x>1),所以 ,
,
则 .
.
点评:也可用数学归纳法证明,为此,先证明 ,即证:lnt<t-1,其中t>1.
,即证:lnt<t-1,其中t>1.
 ,
, ;当△=(b-1)2≠0时,a=1,f(x)=1(x≠0).
;当△=(b-1)2≠0时,a=1,f(x)=1(x≠0).(Ⅱ)由题意知当f(x)=1时,an+1=1,不合题意,所以
 ,
, ,∴
,∴ ,由此可得数列{an}的通项公式.
,由此可得数列{an}的通项公式.(Ⅲ)由题设条件知,
 ,所以
,所以 ,
, ,再用分析法证明Sn>ln(n+1).
,再用分析法证明Sn>ln(n+1).解答:解:(Ⅰ)由
 ,得2a+b=2;
,得2a+b=2;又
 ,有且仅有一个解,
,有且仅有一个解,即ax2+(b-1)x=0,有唯一解满足ax+b≠0.
∵a≠0,∴当△=(b-1)2=0时,b=1,x=0,则
 ,此时
,此时 ,
,又当△=(b-1)2≠0时,
 ,因为ax1+b=1≠0,
,因为ax1+b=1≠0,所以ax2+b=b=0,则a=1,此时

综上所述,
 ,或者f(x)=1(x≠0);
,或者f(x)=1(x≠0);(Ⅱ)a1=1,an+1=f(an)≠1,n∈N*,当f(x)=1时,an+1=1,不合题意,
则
 ,
, ,
,∴
 ,
,则
 ,
,
(Ⅲ)由(Ⅱ)知,

∴
 ,则
,则 ,所以
,所以
设数列{cn}的前n项和为Tn=ln(n+1),则c1=T1=ln2<lne=1
当n≥2时,
 ,要证明
,要证明
令
 ,只要证明:lnt<t-1,其中t>1.
,只要证明:lnt<t-1,其中t>1.令g(x)=x-1-lnx(x≥1),则
 ,所以g(x)在[1,+∞)上是增函数,
,所以g(x)在[1,+∞)上是增函数,则当x>1时,g(x)>g(1)=0,即x-1>lnx(x>1),所以
 ,
,则
 .
.点评:也可用数学归纳法证明,为此,先证明
 ,即证:lnt<t-1,其中t>1.
,即证:lnt<t-1,其中t>1. 
练习册系列答案
相关题目
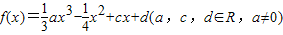 满足f(0)=0,f′(1)=0,且f(x)在R上单调递增.
满足f(0)=0,f′(1)=0,且f(x)在R上单调递增.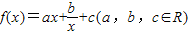 满足f(-1)=0,且对任意x>0都有
满足f(-1)=0,且对任意x>0都有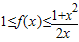 .
.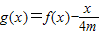 在(0,2]上是减函数,求实数m的取值范围.
在(0,2]上是减函数,求实数m的取值范围.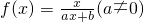 满足f(2)=1,且方程f(x)=x有且仅有一个实数根.
满足f(2)=1,且方程f(x)=x有且仅有一个实数根.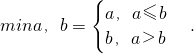 对于(Ⅱ)中的数列{an},令
对于(Ⅱ)中的数列{an},令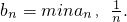 设Sn为数列{bn}的前n项和,求证:Sn>ln(n+1).
设Sn为数列{bn}的前n项和,求证:Sn>ln(n+1).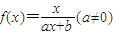 满足f(2)=1,且方程f(x)=x有且仅有一个实数根.
满足f(2)=1,且方程f(x)=x有且仅有一个实数根.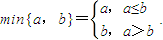 对于(Ⅱ)中的数列{an},令
对于(Ⅱ)中的数列{an},令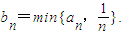 设Sn为数列{bn}的前n项和,求证:Sn>ln(n+1).
设Sn为数列{bn}的前n项和,求证:Sn>ln(n+1).