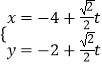Question

【题目】在△ABC中， ，O为平面内一点，且 ，M为劣弧 上一动点，且 ，则p+q的最大值为 ．

Answer 1

【答案】2
【解析】解：∵ ，

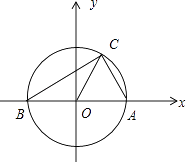
∴O是△ABC的外心．

∵∠A= ，∴∠BOC= ，

设OA=1，A（1，0），B（﹣1，0），C（ ， ），

则 =p =（﹣p+ ， ），

设M（cosα，sinα），则 ≤α≤π，

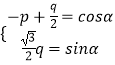∴ ，即 ，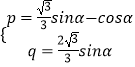

∴p+q= sinα﹣cosα=2sin（α﹣ ），

∵ ≤α≤π，∴ ≤ ≤ ，

∴当 = 时，p+q取得最大值2．

故答案为：2．

由 | | = | | = | | ，可知O是△ABC的外心，以O为坐标原点，建立平面直角坐标系，依据题意得出各点坐标，表示出p，q，结合三角恒等变换可得最大值.