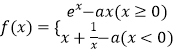Question

【题目】已知椭圆C： + =1（a＞b＞0）的离心率为 ，右焦点为F，右顶点为E，P为直线x= a上的任意一点，且（ + ） =2．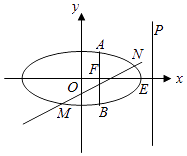

（Ⅰ）求椭圆C的方程；
（Ⅱ）过F垂直于x轴的直线AB与椭圆交于A，B两点（点A在第一象限），动直线l与椭圆C交于M，N两点，且M，N位于直线AB的两侧，若始终保持∠MAB=∠NAB，求证：直线MN的斜率为定值．

Answer 1

【答案】解：（I）F（c，0），E（a，0），设P（ ，y），

则 =（ ，﹣2y）， =（c﹣a，0），

∴（ + ） =（c﹣ ）（c﹣a）=2，

∵椭圆的离心率e= ，∴a=2c，

∴c=1，a=2，b= = ，

∴椭圆C的方程为： =1．

（Ⅱ）直线AB的方程为x=1，代入椭圆方程得y=± ．

∴A（1， ），

设直线l的方程为y=kx+m，代入椭圆方程得：（3+4k2）x2+8kmx+4m2﹣12=0，

由题意可知△＞0，

设M（x1，y1），N（x2，y2），则x1+x2= ，x1x2= ，

∵∠MAB=∠NAB，∴kAM+kAN=0，

∵kAM= = ，kAN= = ，

∴ + =2k+（k+m﹣ ） =2k﹣（k+m﹣ ） =0，

∴（4k﹣2）m+4k2﹣8k+3=0恒成立，

∴ ，解得k= ．

∴直线MN的斜率为定值 ．

【解析】（1）根据题意可得F（c，0），E（a，0），设P（ ，y）,由题中的向量关系，解出a，b，c，从而得到椭圆的方程，（2）由直线AB的方程为x=1，代入椭圆方程，得到A点坐标，设直线l的方程为y=kx+m，设M（x1，y1），N（x2，y2），将直线方程代入椭圆，根据韦达定理可得到x1+x2，x1x2，根据∠MAB=∠NAB，得到kAM+kAN=0，化解后得到（4k﹣2）m+4k2﹣8k+3=0恒成立，从而可得到k为定值.