题目内容
若正实数a,b满足a+b=1,则
- A.
 有最大值4
有最大值4 - B.ab有最小值

- C.
 有最大值
有最大值
- D.a2+b2有最小值

C
分析:由于 =
=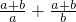 =2+
=2+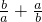 ≥4,故A不正确.
≥4,故A不正确.
由基本不等式可得 a+b=1≥2 ,可得 ab≤
,可得 ab≤ ,故B不正确.
,故B不正确.
由于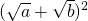 =1+2
=1+2 ≤2,故
≤2,故  ≤
≤ ,故 C 正确.
,故 C 正确.
由a2+b2 =(a+b)2-2ab≥1- =
= ,故D不正确.
,故D不正确.
解答:∵正实数a,b满足a+b=1,
∴ =
=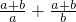 =2+
=2+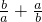 ≥2+2=4,故
≥2+2=4,故 有最小值4,故A不正确.
有最小值4,故A不正确.
由基本不等式可得 a+b=1≥2 ,∴ab≤
,∴ab≤ ,故ab有最大值
,故ab有最大值 ,故B不正确.
,故B不正确.
由于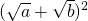 =a+b+2
=a+b+2 =1+2
=1+2 ≤2,∴
≤2,∴ ≤
≤ ,故
,故 有最大值为
有最大值为 ,故C正确.
,故C正确.
∵a2+b2 =(a+b)2-2ab=1-2ab≥1- =
= ,故a2+b2有最小值
,故a2+b2有最小值 ,故D不正确.
,故D不正确.
故选C.
点评:本题考查基本不等式的应用,注意检验等号成立的条件,式子的变形是解题的关键.
分析:由于
 =
=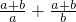 =2+
=2+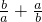 ≥4,故A不正确.
≥4,故A不正确.由基本不等式可得 a+b=1≥2
 ,可得 ab≤
,可得 ab≤ ,故B不正确.
,故B不正确.由于
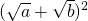 =1+2
=1+2 ≤2,故
≤2,故  ≤
≤ ,故 C 正确.
,故 C 正确.由a2+b2 =(a+b)2-2ab≥1-
 =
= ,故D不正确.
,故D不正确.解答:∵正实数a,b满足a+b=1,
∴
 =
=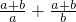 =2+
=2+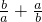 ≥2+2=4,故
≥2+2=4,故 有最小值4,故A不正确.
有最小值4,故A不正确.由基本不等式可得 a+b=1≥2
 ,∴ab≤
,∴ab≤ ,故ab有最大值
,故ab有最大值 ,故B不正确.
,故B不正确.由于
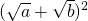 =a+b+2
=a+b+2 =1+2
=1+2 ≤2,∴
≤2,∴ ≤
≤ ,故
,故 有最大值为
有最大值为 ,故C正确.
,故C正确.∵a2+b2 =(a+b)2-2ab=1-2ab≥1-
 =
= ,故a2+b2有最小值
,故a2+b2有最小值 ,故D不正确.
,故D不正确.故选C.
点评:本题考查基本不等式的应用,注意检验等号成立的条件,式子的变形是解题的关键.

练习册系列答案
相关题目
若正实数a,b满足a+b=1,则( )
A、
| ||||||
B、ab有最小值
| ||||||
C、
| ||||||
D、a2+b2有最小值
|
若正实数a,b满足a+b=1,则
+
的最小值是( )
| 1 |
| a |
| 4 |
| b |
| A、4 | B、6 | C、8 | D、9 |