题目内容
定义在区间
上的连续函数
的导函数为
，如果
使得
，则称
为区间上的“中值点”.下列函数：①
；②
；③
；④
在区间
上“中值点”多于一个的函数序号为 .
①④
解析试题分析：根据“中值点”的定义，设为区间上的中值点，则
，①中
，因为
，此时区间的任一实数都为“中值点”；对于②，
即
；对于③
即
；对于④
即
；综上可知，选①④.
考点：1.新定义；2.导数的计算.
练习册系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
在区间
上是增函数，则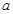
的范围是 .（用区间来表示）
有极大值和极小值，则实数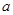
的取值范围是 
在
处的导数
= .
处的切线平行于直线
的坐标是_______.
在x=4处的导数
= .
x3－
x2－40x(x>0)，为使耗电量最小，则速度应定为________．