题目内容
设数列{an}(n∈N)满足a0=0,a1=2,且对一切n∈N,有an+2=2an+1-an+2.
(I)求数列{an}的通项公式;
(II)当n∈N+时,令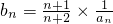 ,Sn是数列{bn}的前n项和,求证:
,Sn是数列{bn}的前n项和,求证: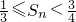 .
.
解:(I)由an+2-an+1=an+1-an+2可得:数列{an+1-an}为等差数列,且首项a1-a0=2-0=2,公差为2(3分)
∴an-an-1=(a1-a0)+2(n-1)=2+2(n-1)=2n(4分)
∴an=a1+(a2-a1)+(a3-a2)+…+(an-an-1)=2+4+6+…+2n= =n(n+1)(6分)
=n(n+1)(6分)
(II)由(I)可知: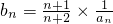 =-
=-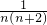 =
= (
( -
- )
)
∴Sn=b1+b2+…+bn= [(1-
[(1- )+(
)+( -
- )+…+(
)+…+( -
- )]=
)]= (1+
(1+ -
- -
- )<
)< (10分)
(10分)
易知:Sn在n∈N*时,单调递增,
∴Sn≥S1= (11分)
(11分)
∴ ≤Sn<
≤Sn< (12分)
(12分)
分析:(I)由an+2-an+1=an+1-an+2得,数列{an+1-an}为等差数列,且首项a1=2,公差为2,由此能求出数列{an}的通项公式;
(II)确定数列的通项,利用裂项法求和,借助于单调性,即可得到结论.
点评:本题考查数列递推式,考查叠加法的运用,考查数列求和,解题的关键是确定数列的通项,属于中档题.
∴an-an-1=(a1-a0)+2(n-1)=2+2(n-1)=2n(4分)
∴an=a1+(a2-a1)+(a3-a2)+…+(an-an-1)=2+4+6+…+2n=
 =n(n+1)(6分)
=n(n+1)(6分)(II)由(I)可知:
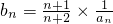 =-
=-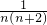 =
= (
( -
- )
)∴Sn=b1+b2+…+bn=
 [(1-
[(1- )+(
)+( -
- )+…+(
)+…+( -
- )]=
)]= (1+
(1+ -
- -
- )<
)< (10分)
(10分)易知:Sn在n∈N*时,单调递增,
∴Sn≥S1=
 (11分)
(11分)∴
 ≤Sn<
≤Sn< (12分)
(12分)分析:(I)由an+2-an+1=an+1-an+2得,数列{an+1-an}为等差数列,且首项a1=2,公差为2,由此能求出数列{an}的通项公式;
(II)确定数列的通项,利用裂项法求和,借助于单调性,即可得到结论.
点评:本题考查数列递推式,考查叠加法的运用,考查数列求和,解题的关键是确定数列的通项,属于中档题.

练习册系列答案
相关题目