题目内容
已知:函数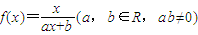 ,
, 有唯一的根.
有唯一的根.(1)求a,b的值;
(2)数列{an}对n≥2,n∈N总有an=f(an-1),a1=1;求证
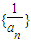 为等差数列,并求出{an}的通项公式.
为等差数列,并求出{an}的通项公式.(3)是否存在这样的数列{bn}满足:{bn}为{an}的子数列(即{bn}中的每一项都是{an}的项)且{bn}为无穷等比数列,它的各项和为
 .若存在,找出一个符合条件的数列{bn},写出它的通项公式;若不存在,说明理由.
.若存在,找出一个符合条件的数列{bn},写出它的通项公式;若不存在,说明理由.
【答案】分析:(1)根据f(2)的值建立关于a和b的等量关系,
解法一:根据f(x)=x 有唯一根,可得ax2+(b-1)x=0有唯一根,利用判别式进行求解,求出a和b的值;
解法二:根据f(x)=x 有唯一根,可得x(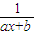 -1)=0,解得一根为0,从而
-1)=0,解得一根为0,从而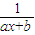 -1=0的根也是x=0,可求出a和b的值;
-1=0的根也是x=0,可求出a和b的值;
(2)将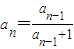 取倒数,化简可得{
取倒数,化简可得{ }为等差数列,从而求出{an}的通项公式.
}为等差数列,从而求出{an}的通项公式.
(3)设{bn} 的首项为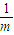 ,公比为q,然后求出这个无穷等比数列的各项和可得到m和q的等量关系,然后任意求出一组符合题意数列即可.
,公比为q,然后求出这个无穷等比数列的各项和可得到m和q的等量关系,然后任意求出一组符合题意数列即可.
解答:解:(1)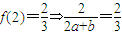 (1分)
(1分)
解法一:f(x)=x 有唯一根,所以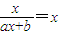 即ax2+(b-1)x=0有唯一根,(1分)
即ax2+(b-1)x=0有唯一根,(1分)
∴△=(b-1)2=0,(1分)
b=1 a=1 (1分)
有 b=1 a=1 得:方程的根为:x=0(1分)
经检验x=0是原方程的根(1分)
解法二: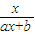 =x
=x
x(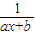 -1)=0(1分)
-1)=0(1分)
x1=0,因为方程有唯一的根(1分)
即: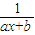 -1=0的根也是x=0,(1分)
-1=0的根也是x=0,(1分)
得b=1 a=1 (1分)
经检验x=0是原方程的根(1分)
(2)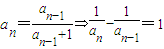 (2分)
(2分)
∴{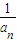 }为等差数列(1分)
}为等差数列(1分)
∴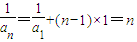 (2分)
(2分)
所以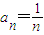 (1分)
(1分)
(3)设{bn} 的首项为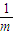 ,公比为q (
,公比为q (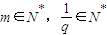 )
)
所以这个无穷等比数列的各项和为:
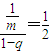 ,
,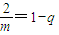 ;
;
当m=3 时,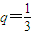 ,
,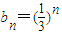 ;
;
当 ,
,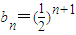 (6分)
(6分)
点评:本题主要考查了等差数列的判定和数列的求和,同时考查了方程的根的有关问题,属于中档题.
解法一:根据f(x)=x 有唯一根,可得ax2+(b-1)x=0有唯一根,利用判别式进行求解,求出a和b的值;
解法二:根据f(x)=x 有唯一根,可得x(
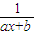 -1)=0,解得一根为0,从而
-1)=0,解得一根为0,从而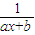 -1=0的根也是x=0,可求出a和b的值;
-1=0的根也是x=0,可求出a和b的值;(2)将
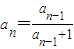 取倒数,化简可得{
取倒数,化简可得{ }为等差数列,从而求出{an}的通项公式.
}为等差数列,从而求出{an}的通项公式.(3)设{bn} 的首项为
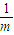 ,公比为q,然后求出这个无穷等比数列的各项和可得到m和q的等量关系,然后任意求出一组符合题意数列即可.
,公比为q,然后求出这个无穷等比数列的各项和可得到m和q的等量关系,然后任意求出一组符合题意数列即可.解答:解:(1)
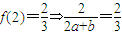 (1分)
(1分)解法一:f(x)=x 有唯一根,所以
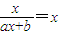 即ax2+(b-1)x=0有唯一根,(1分)
即ax2+(b-1)x=0有唯一根,(1分) ∴△=(b-1)2=0,(1分)
b=1 a=1 (1分)
有 b=1 a=1 得:方程的根为:x=0(1分)
经检验x=0是原方程的根(1分)
解法二:
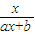 =x
=x x(
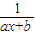 -1)=0(1分)
-1)=0(1分)x1=0,因为方程有唯一的根(1分)
即:
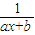 -1=0的根也是x=0,(1分)
-1=0的根也是x=0,(1分)得b=1 a=1 (1分)
经检验x=0是原方程的根(1分)
(2)
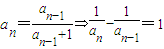 (2分)
(2分) ∴{
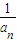 }为等差数列(1分)
}为等差数列(1分)∴
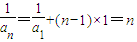 (2分)
(2分)所以
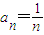 (1分)
(1分)(3)设{bn} 的首项为
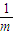 ,公比为q (
,公比为q (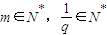 )
)所以这个无穷等比数列的各项和为:
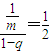 ,
,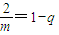 ;
;当m=3 时,
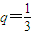 ,
,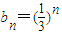 ;
;当
 ,
,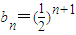 (6分)
(6分)点评:本题主要考查了等差数列的判定和数列的求和,同时考查了方程的根的有关问题,属于中档题.

练习册系列答案
相关题目
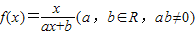 ,
,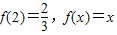 有唯一的根.
有唯一的根. .若存在,找出所有符合条件的数列{bn},写出它的通项公式,并说明理由;若不存在,也需说明理由.
.若存在,找出所有符合条件的数列{bn},写出它的通项公式,并说明理由;若不存在,也需说明理由.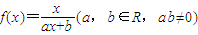 ,
,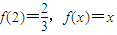 有唯一的根.
有唯一的根. .若存在,找出所有符合条件的数列{bn},写出它的通项公式,并说明理由;若不存在,也需说明理由.
.若存在,找出所有符合条件的数列{bn},写出它的通项公式,并说明理由;若不存在,也需说明理由.