Question

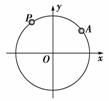
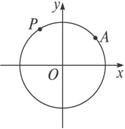
已知P在1秒钟内转过的角度为θ（0°＜θ＜180°），经过2秒钟到达第三象限，经过14秒钟后又恰好回到出发点，则θ=

 

．

Answer 1

分析：由k•360°+180°＜2θ＜k•360°+270°（k∈Z），及14θ=n•360°（n∈Z），解出θ的大小．

解答：解：∵0°＜θ＜180°且
k•360°+180°＜2θ＜k•360°+270°（k∈Z），
则必有k=0，于是90°＜θ＜135°，
又14θ=n•360°（n∈Z），
∴θ=

n

7

×180°，
∴90°＜

n

7

•180°＜135°，

7

2

＜n＜

21

4

，
∴n=4或5，故θ=

720°

7

 或

900°

7

．
故答案为：

720°

7

 或

900°

7

．

点评：本题考查象限角、终边相同的角的概念和求法，关键是依据题中的已知条件列出关于θ 的等式、不等式，体现了转化数学思想．