题目内容
已知函数![]()
(1)试求![]() 的值;
的值;
(2)若数列![]()
![]() ,求数列{an}的通项公式;
,求数列{an}的通项公式;
(3)若数列{bn}满足bn=2n+1·an,Sn是数列{bn}前n项的和,是否存在正实数k,使不等式knSn>4bn对于一切的n∈N*恒成立?若存在指出k的取值范围,并证明;若不存在说明理由.
答案:
解析:
解析:
解:(1)∵![]() =
=![]() +
+![]() =
=![]() +
+![]() =1
=1
∴![]() 5分
5分
(2)∵![]() ①
①
∴![]() ②
②
由(Ⅰ),知![]()
∴①+②,得![]() 10分
10分
(3)∵![]() ,∴
,∴![]()
∴![]() ①
①
![]() ②
②
①-②得![]()
即![]() 12分
12分
要使得不等式![]() 恒成立,即
恒成立,即![]() 对于一切的
对于一切的![]() 恒成立,
恒成立,![]()
设![]()
当![]() 时,由于对称轴直线
时,由于对称轴直线![]() ,且
,且![]() ,而函数
,而函数![]() 在
在![]() 是增函数,∴不等式
是增函数,∴不等式![]() 恒成立
恒成立
即当![]()
![]()
![]() 时,不等式
时,不等式![]() 对于一切的
对于一切的![]() 恒成立 16分
恒成立 16分
[采分点12分后]或解:分离参数法:![]() 对一切的
对一切的![]() 恒成立,
恒成立,
令![]() ,用基本不等式法可求
,用基本不等式法可求![]() =4
=4
所以![]()
![]()
![]()

练习册系列答案
相关题目

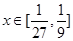 ,求函数
,求函数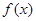 最大值和最小值;
最大值和最小值;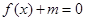 有两根
有两根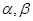 ,试求
,试求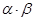 的值.
的值.
 有唯一解,求a的取值范围.
有唯一解,求a的取值范围.