题目内容
已知函数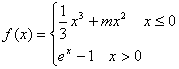
(I)讨论函数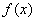 的极值情况;
的极值情况;
(Ⅱ)设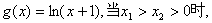 试比较
试比较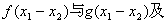
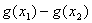 三者的大小;并说明理由。
三者的大小;并说明理由。
【答案】
【解析】(1)当x > 0时,f (x) = ex– 1在(0,+∞)单调递增,且f (x) > 0;
当x≤0时,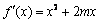 .
.
①若m = 0,f ′(x) = x2≥0, f (x) =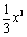 在(–∞,0)上单调递增,且
在(–∞,0)上单调递增,且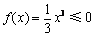 .
.
又f (0) = 0,∴f (x)在R上是增函数,无极植;
②若m < 0,f ′(x) = x(x + 2m) >0,则f (x) = 在(–∞,0)单调递增,同①可知f (x)在R上也是增函数,无极值; 4分
在(–∞,0)单调递增,同①可知f (x)在R上也是增函数,无极值; 4分
③若m > 0,f (x)在(–∞,–2m)上单调递增,在(–2m,0)单调递减,
又f (x)在(0, +∞)上递增,故f (x)有极小值f (0) = 0,f (x)有极大值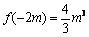 . 6分
. 6分
(2)当x > 0时,先比较ex – 1与ln(x + 1)的大小,
设h(x) = ex – 1–ln(x + 1) (x >0)
h′(x) =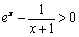 恒成立
恒成立
∴h(x)在(0,+∞)是增函数,h(x) > h (0) = 0
∴ex – 1–ln(x + 1) > 0即ex – 1 > ln(x + 1)
也就是f (x) > g (x) ,对任意x > 0成立.
故当x1 – x2 > 0时,f (x1 – x2) > g (x1 – x2) 10分
再比较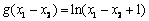 与g(x1)–g
(x2)= ln(x1 + 1)–ln(x2 + 1)的大小.
与g(x1)–g
(x2)= ln(x1 + 1)–ln(x2 + 1)的大小.
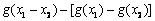 =
=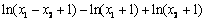
=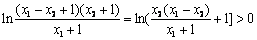
∴g (x1 – x2) > g (x1) –g (x2)
∴f (x1 – x2)> g (x1 – x2) > g (x1) –g (x2) . 12分

练习册系列答案
相关题目

 (0,+∞),且x1≠x2,都有
(0,+∞),且x1≠x2,都有 恒成立.若存在,求出a的取值范围;若不存在,说明理由.
恒成立.若存在,求出a的取值范围;若不存在,说明理由.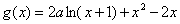
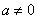 时,讨论函数
时,讨论函数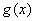 的单调性:
的单调性: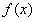 的图像上存在不同两点
的图像上存在不同两点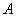 ,
,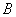 ,设线段
,设线段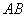 的中点为
的中点为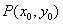 ,使得
,使得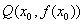 处的切线
处的切线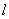 与直线
与直线