题目内容
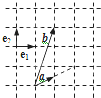 如图所示,若向量
如图所示,若向量 1、
1、 2是一组单位正交向量,则向量2
2是一组单位正交向量,则向量2 +
+ 在平面直角坐标系中的坐标为
在平面直角坐标系中的坐标为
- A.(3,4)
- B.(2,4)
- C.(3,4)或(4,3)
- D.(4,2)或(2,4)
A
分析:以向量 、
、 公共的起点为坐标原点,建立如图坐标系.可得向量
公共的起点为坐标原点,建立如图坐标系.可得向量 =(1,
=(1, )且
)且 =(1,3),结合向量坐标的线性运算性质,即可得到向量2
=(1,3),结合向量坐标的线性运算性质,即可得到向量2 +
+ 在平面直角坐标系中的坐标.
在平面直角坐标系中的坐标.
解答: 以向量
以向量 、
、 公共的起点为坐标原点,建立如图坐标系
公共的起点为坐标原点,建立如图坐标系
∵ 1=(1,0),
1=(1,0), 2=(0,1)
2=(0,1)
∴2 =(2,1),得
=(2,1),得 =(1,
=(1, ),
),
∵ =(1,3),
=(1,3),
∴2 +
+ =2(1,
=2(1, )+(1,3)=(3,4)
)+(1,3)=(3,4)
即2 +
+ 在平面直角坐标系中的坐标为(3,4)
在平面直角坐标系中的坐标为(3,4)
故选:A
点评:本题给出垂直的单位向量,求第三个向量在这组向量作为基底下的坐标,着重考查了平面向量的正交分解及坐标表示的知识,属于基础题.
分析:以向量
 、
、 公共的起点为坐标原点,建立如图坐标系.可得向量
公共的起点为坐标原点,建立如图坐标系.可得向量 =(1,
=(1, )且
)且 =(1,3),结合向量坐标的线性运算性质,即可得到向量2
=(1,3),结合向量坐标的线性运算性质,即可得到向量2 +
+ 在平面直角坐标系中的坐标.
在平面直角坐标系中的坐标.解答:
 以向量
以向量 、
、 公共的起点为坐标原点,建立如图坐标系
公共的起点为坐标原点,建立如图坐标系∵
 1=(1,0),
1=(1,0), 2=(0,1)
2=(0,1)∴2
 =(2,1),得
=(2,1),得 =(1,
=(1, ),
),∵
 =(1,3),
=(1,3),∴2
 +
+ =2(1,
=2(1, )+(1,3)=(3,4)
)+(1,3)=(3,4)即2
 +
+ 在平面直角坐标系中的坐标为(3,4)
在平面直角坐标系中的坐标为(3,4)故选:A
点评:本题给出垂直的单位向量,求第三个向量在这组向量作为基底下的坐标,着重考查了平面向量的正交分解及坐标表示的知识,属于基础题.

练习册系列答案
相关题目
 已知点F(1,0),直线l:x=2,设动点P到直线l的距离为d,已知
已知点F(1,0),直线l:x=2,设动点P到直线l的距离为d,已知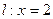 ,设动点P到直线
,设动点P到直线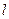 的距离为
的距离为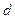 ,已知
,已知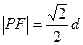 ,且
,且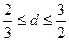 .
.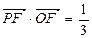 ,求向量
,求向量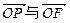 的夹
的夹 角;
角; ,点M满足
,点M满足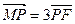 ,且线段MG的垂直平分线经过点P,求
,且线段MG的垂直平分线经过点P,求 的面积
的面积 中,
中, 平面
平面 ,底面
,底面 .
. 时,求证:
时,求证: ;
; 边上有且只有一个点
边上有且只有一个点 ,使得
,使得 ,求此时二面角
,求此时二面角 的余弦值.
的余弦值.


 ,
, ………………2分
………………2分 ,得证。
,得证。 ,只要
,只要
 ,即
,即 ………6分
………6分
 ,所以
,所以 平面PAD的法向量
平面PAD的法向量
 的大小与二面角A-PD-Q的大小相等所以
的大小与二面角A-PD-Q的大小相等所以

 ………………3分
………………3分
 ,设动点P到直线
,设动点P到直线 的距离为
的距离为 ,已知
,已知 ,且
,且 .
.
 ,求向量
,求向量 的夹角;
的夹角; ,点M满足
,点M满足 ,且线段MG的垂直平分线经过点P,求
,且线段MG的垂直平分线经过点P,求 的面积.
的面积.