题目内容
解不等式：?(1)|x+1|>2－x;?
(2)|3x－4|<x－1.?
解：(1)原不等式等价于?
①
或②
而①
x>
;?
②
无解.?
∴原不等式的解集为{x|x>
}.?
(2)∵当x－1≤0时，不等式无解,?
∴原不等式可变形为
化简，得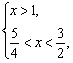
解得
<x<
.?
∴原不等式的解集为{x|
<x<
}.?
点评：形如|f(x)|>g(x)的不等式，可根据绝对值的意义化为不等式组：?
或
来求解.?
不等式|f(x)|<g(x)可化为
或
来求解.
练习册系列答案
相关题目