Question

已知平面区域

x≥0 y≥0 x+2y-4≤0

  恰好被面积最小的⊙C：（x-a）²+（y-b）²=r²及其内部所覆盖．
（1）试求⊙C的方程．
（2）若斜率为1的直线l与⊙C交于不同的两点A、B，且满足CA⊥CB，求直线l的方程．

Answer 1

分析：（1）画出可行域，求出三角形区域OMN的外接圆满足条件；
（2）设直线l的方程为y=x+m，交点A（x₁，y₁），B（x₂，y₂）．与⊙C的方程联立得到△＞0即根与系数的关系，利用向量垂直与数量积的关系即可求出．

解答：解：（1）画出平面区域

x≥0 y≥0 x+2y-4≤0

，如图所示的直角△OMN，
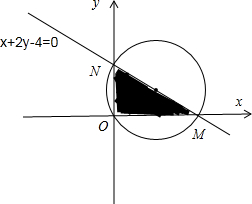 恰好被面积最小的⊙C：（x-a）²+（y-b）²=r²及其内部所覆盖，则⊙C是△OMN的外接圆．
由x+2y-4=0与x轴相交于点M（4，0），与y轴相交于点N（0，2）．
∴|MN|=

22+42

=2

5

．
因此Rt△OMN的外接圆的直径为2

5

，圆心为斜边MN的中点C（2，1）．
故⊙C的方程为：（x-2）²+（y-1）²=5．
（2）设直线l的方程为y=x+m，
交点A（x₁，y₁），B（x₂，y₂）．
联立

y=x+m (x-2)2+(y-1)2=5

，化为2x²+2（m-3）x+m²-2m=0．
∵直线l与⊙C有两个不同的交点，∴△＞0，化为＞m²+2m-9＜0．（*）
∴x₁+x₂=3-m，x1x2=

m2-2m

2

．
∵CA⊥CB．
∴

CA

•

CB

=（x₁-2，y₁-1）•（x₂-2，y₂-1）=（x₁-2）（x₂-2）+（y₁-1）（y₂-1）=x₁x₂-2（x₁+x₂）+4+（x₁+m-1）（x₂+m-1）
=2x₁x₂+（m-3）（x₁+x₂）+（m-1）²+4=0．
代入可得m²-2m+（m-3）（3-m）+（m-1）²+4=0，化为m²+2m-4=0，解得m=-1±

5

．满足（*）．
∴满足条件的直线l的方程为y=x+(-1±

5

)．

点评：本题考查了线性规划的可行域、三角形的外接圆、直线与圆相交问题转化为方程联立得到△＞0即根与系数的关系、向量垂直与数量积的关系等基础知识与基本技能方法，属于难题．