题目内容
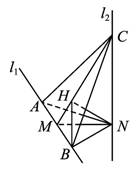
如图,l1,l2是互相垂直的异面直线,MN是它们的公垂线段.点A,B在l1上,C在l2上,AM=MB=MN.(1)证明AC⊥NB;
(2)若∠ACB=60°,求NB与平面ABC所成角的余弦值.

(1)证明:由已知l2⊥MN,l2⊥l1,MN∩l1=M,可得l2⊥平面ABN.
由已知MN⊥l1,AM=MB=MN,可知AN=NB且AN⊥NB.
又AN为AC在平面ABN内的射影,
∴AC⊥NB.
(2)解:∵Rt△CNA≌Rt△CNB,

∴AC=BC.又已知∠ACB=60°,
∴△ABC为正三角形.
∵Rt△ANB≌Rt△CNB,
∴NC=NA=NB,因此N在平面ABC内的射影H是正三角形ABC的中心.连结BH,∠NBH为NB与平面ABC所成的角.
在Rt△NHB中,cos∠NBH=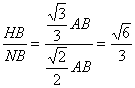 .
.

练习册系列答案
相关题目