题目内容
已知函数f(x)=x2-2x+loga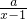 在(1,
在(1, )内恒小于零,则实数a的取值范围是
)内恒小于零,则实数a的取值范围是
- A.
 ≤a<1
≤a<1 - B.0<a

- C.0
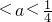
- D.a≥

A
分析:求出函数f(x)的定义域,f(x)在(1, )内恒小于零等价于f(x)max<0,求出导数f′(x),分0<a<1,a>1两种情况利用导数求出f(x)的最大值即可.
)内恒小于零等价于f(x)max<0,求出导数f′(x),分0<a<1,a>1两种情况利用导数求出f(x)的最大值即可.
解答:f(x)=x2-2x+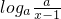 ,
,
因为a>0,且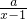 >0,所以定义域:{x|x>1}.
>0,所以定义域:{x|x>1}.
f'(x)=2x-2-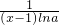 ,
,
①当0<a<1时,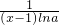 <0,所以在x∈(1,
<0,所以在x∈(1, )时f'(x)>0,函数f(x)在(1,
)时f'(x)>0,函数f(x)在(1, )上是增函数,
)上是增函数,
要满足题意,须f( )≤0,即:
)≤0,即: -3+loga(2a)≤0,即:loga2≤-
-3+loga(2a)≤0,即:loga2≤- ,
,
解得:a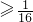 ,又0<a<1,所以
,又0<a<1,所以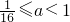 .
.
②当a>1时,由f'(x)=0得:x=1+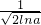 ,
,
当x<1+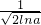 时,f'(x)<0,当x>1+
时,f'(x)<0,当x>1+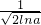 时,f'(x)>0,
时,f'(x)>0,
由此得函数f(x)在x<1+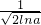 时是减函数,在x>1++
时是减函数,在x>1++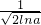 时是增函数,
时是增函数,
而f( )=
)= -3+loga(2a)=loga2+
-3+loga(2a)=loga2+ >0,
>0,
所以a>1时,不能保证在(1, )内f(x)恒小于0,
)内f(x)恒小于0,
故a>1不合题意,舍去.
综上,所求实数a的取值范围为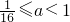 .
.
故选A.
点评:本题考查应用导数求函数的最值,考查不等式恒成立,考查分类讨论思想,解决本题的关键是利用导数求出函数的最大值.
分析:求出函数f(x)的定义域,f(x)在(1,
 )内恒小于零等价于f(x)max<0,求出导数f′(x),分0<a<1,a>1两种情况利用导数求出f(x)的最大值即可.
)内恒小于零等价于f(x)max<0,求出导数f′(x),分0<a<1,a>1两种情况利用导数求出f(x)的最大值即可.解答:f(x)=x2-2x+
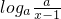 ,
,因为a>0,且
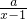 >0,所以定义域:{x|x>1}.
>0,所以定义域:{x|x>1}.f'(x)=2x-2-
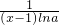 ,
,①当0<a<1时,
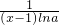 <0,所以在x∈(1,
<0,所以在x∈(1, )时f'(x)>0,函数f(x)在(1,
)时f'(x)>0,函数f(x)在(1, )上是增函数,
)上是增函数,要满足题意,须f(
 )≤0,即:
)≤0,即: -3+loga(2a)≤0,即:loga2≤-
-3+loga(2a)≤0,即:loga2≤- ,
,解得:a
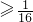 ,又0<a<1,所以
,又0<a<1,所以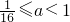 .
.②当a>1时,由f'(x)=0得:x=1+
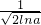 ,
,当x<1+
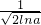 时,f'(x)<0,当x>1+
时,f'(x)<0,当x>1+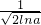 时,f'(x)>0,
时,f'(x)>0,由此得函数f(x)在x<1+
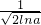 时是减函数,在x>1++
时是减函数,在x>1++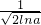 时是增函数,
时是增函数,而f(
 )=
)= -3+loga(2a)=loga2+
-3+loga(2a)=loga2+ >0,
>0,所以a>1时,不能保证在(1,
 )内f(x)恒小于0,
)内f(x)恒小于0,故a>1不合题意,舍去.
综上,所求实数a的取值范围为
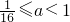 .
.故选A.
点评:本题考查应用导数求函数的最值,考查不等式恒成立,考查分类讨论思想,解决本题的关键是利用导数求出函数的最大值.

练习册系列答案
相关题目
 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<| π |
| 2 |
A、f(x)=2sin(πx+
| ||
B、f(x)=2sin(2πx+
| ||
C、f(x)=2sin(πx+
| ||
D、f(x)=2sin(2πx+
|