Question

（13分）设函数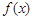=x+ax2+blnx，曲线y=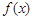过P（1,0），且在P点处的切斜线率为2．

（I）求a，b的值；（II）证明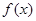：≤2x-2．

 

Answer 1

【答案】

（ I）   

（II）设则

而

【解析】本试题主要是考查了导数在研究函数中的运用，研究切线的斜率和不等式的证明综合运用。

（1）由于，结合已知条件可知得到参数a,b的值。

（2）根据，由（I）知

设构造函数求解导数判定最大值得到证明。

解：（ I）   

由已知条件得，解得   

（II），由（I）知

设则

而