题目内容

函数f（x）=ax2+4（a+1）x-3在[2，+∞]上递减，则a的取值范围是 ________．


分析：本题要对a进行讨论，当a等于0时，f（x）=4x-3，不符合题意；当a≠0时，函数f（x）=ax2+4（a+1）x-3在[2，+∞]上递减，则a必小于0，并且对称轴必在x=2的左边，即
解答：当a=0时
f（x）=4x-3，不符合题意
当a≠0时
∵函数f（x）=ax2+4（a+1）x-3在[2，+∞]上递减
∴
解之得：a
故答案为：
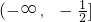
点评：本题考查了二次函数的性质，分类讨论的思想，属于基础题．
练习册系列答案
相关题目
已知二次函数f（x）=ax2+bx（a，b是常数，且a≠0），f（2）=0，且方程f（x）=x有两个相等的实数根．
（1）求f（x）的解析式；
（2）当x∈[0，3]时，求函数f（x）的值域．
设函数f（x）=ax2+bx+c（a≠0），曲线y=f（x）通过点（0，2a+3），且在x=1处的切线垂直于y轴．
（Ⅰ）用a分别表示b和c；
（Ⅱ）当bc取得最大值时，写出y=f（x）的解析式；
（Ⅲ）在（Ⅱ）的条件下，g（x）满足
43
f(x)-6=（x-2）g（x）（x＞2），求g（x）的最大值及相应x值．
已知函数f（x）=ax2+ln（x+1）．
（Ⅰ）当a=
1
4
时，求函数f（x）的单调区间；
（Ⅱ）当x∈[0，+∞）时，不等式f（x）≤x恒成立，求实数a的取值范围；
（Ⅲ）求证：(1+
2
2×3
)×(1+
4
3×5
)×(1+
8
5×9
)…(1+
2n
(2n-1+1)(2n+1)
)＜e（其中，n∈N*，e是自然对数的底数）
已知实数a，b，c（a≠0）满足
a
m+2
+
b
m+1
+
c
m
=0(m＞0)，对于函数f（x）=ax2+bx+c，af(
m
m+1
)与0的大小关系是（　　）
已知函数f（x）=ax2+bx+1（a，b为实数），x∈R，F(x)=
f(x)(x＞0)
-f(x)(x＜0)

（1）若f（-1）=0，且函数f（x）的值域为[0，+∞），求F（x）的表达式；
（2）在（1）的条件下，当x∈[-2，2]时，g（x）=f（x）-kx是单调函数，求实数k的取值范围；
（3）设m•n＜0，m+n＞0，a＞0且f（x）为偶函数，判断F（m）+F（n）能否大于零．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网