题目内容
在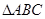 中,
中,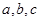 分别为
分别为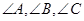 的对边,已知
的对边,已知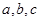 成等比数列,且
成等比数列,且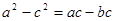 .
.
求:(1)A的大小; (2)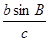 的值.
的值.
 中,
中, 分别为
分别为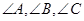 的对边,已知
的对边,已知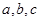 成等比数列,且
成等比数列,且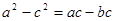 .
.求:(1)A的大小; (2)
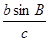 的值.
的值.(1) 





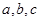 成等比数列,
成等比数列, ,又因为
,又因为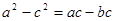 ,得
,得
用余弦定理解得角;
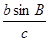 化为角或边,
化为角或边,
解析:由已知得
 ,因此
,因此 可化为
可化为 ……3分
……3分
 ………………………5分
………………………5分 法一:在
法一:在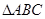 中,由正弦定理得
中,由正弦定理得 ……………7分
……………7分
 .……………………10分
.……………………10分法二:在
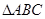 中,由面积公式得
中,由面积公式得 .
.



练习册系列答案
 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
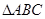 中,角
中,角 ,
,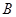 ,
,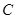 所对的边长分别是
所对的边长分别是 ,
,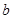 ,
,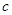 . 满足
. 满足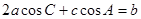 .
.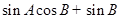 的最大值.
的最大值.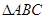 的内角
的内角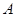 、
、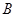 、
、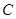 的对边分别为
的对边分别为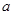 、
、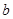 、
、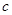 ,
,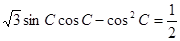 ,且
,且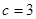
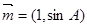 与
与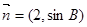 共线,求
共线,求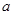 ,
,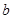 ,
,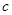 分别为
分别为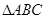 三个内角
三个内角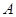 ,
,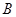 ,
,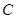 的对边,
的对边,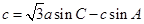 .
.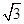 ,求
,求 中,已知
中,已知
 ,面积
,面积 ,
, 是
是 的距离分别是
的距离分别是
 的取值范围.
的取值范围. 是底部
是底部 不可到达的一个塔型建筑物,
不可到达的一个塔型建筑物, 为塔的最高点.现需在对岸测出塔高
为塔的最高点.现需在对岸测出塔高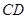 ,使
,使 三点不在同一
三点不在同一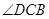 及
及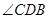 的大小(分别用
的大小(分别用 表示测得的数据)以及
表示测得的数据)以及 间的距离(用
间的距离(用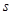 表示测得的数据),另外需在点
表示测得的数据),另外需在点 测得塔顶
测得塔顶 表示测量的数据),就可以求得塔高
表示测量的数据),就可以求得塔高 ,使
,使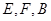 三点在同一条直线上.在
三点在同一条直线上.在 处分别测得塔顶
处分别测得塔顶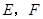 按从左到右的方向标注;③求塔高
按从左到右的方向标注;③求塔高

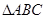 中,
中, 分别是角
分别是角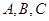 的对边,若
的对边,若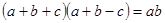 ,则
,则 = .
= . 中,A=
中,A= ,BC=
,BC= ,D是AB边上的一点,且BD=2,CD=
,D是AB边上的一点,且BD=2,CD= ,则AC的长为
,则AC的长为