Question

【题目】已知函数f（x）= （x+ ），g（x）= （x﹣ ）．
（1）求函数h（x）=f（x）+2g（x）的零点；
（2）求函数F（x）=[f（x）]2n﹣[g（x）]2n（n∈N*）的最小值．

Answer 1

【答案】
（1）解：∵f（x）= （x+ ），g（x）= （x﹣ ），

∴h（x）=f（x）+2g（x）= ，

由 ，得3x2=1，

∴x= ．

即函数h（x）=f（x）+2g（x）的零点为：

（2）解：F（x）=[f（x）]2n﹣[g（x）]2n=

=

=

≥ = ．

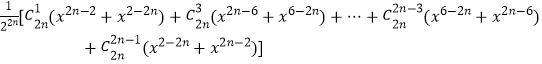
当且仅当x=±1时等号成立．

∴函数F（x）=[f（x）]2n﹣[g（x）]2n（n∈N*）的最小值为1

【解析】（1）直接由h（x）=f（x）+2g（x）=0求解关于x的方程得答案；（2）由F（x）=[f（x）]2n﹣[g（x）]2n= ，展开二项式定理，重新组合后利用基本不等式转化，再由二项式系数的性质求得F（x）的最小值．
【考点精析】解答此题的关键在于理解函数的最值及其几何意义的相关知识，掌握利用二次函数的性质（配方法）求函数的最大（小）值；利用图象求函数的最大（小）值；利用函数单调性的判断函数的最大（小）值．