题目内容
体育课进行篮球投篮达标测试,规定:每位同学有5次投篮机会,若投中3次则“达标”;为节省测试时间,同时规定:①若投篮不到5次已达标,则停止投篮;②投篮过程中,若已有3次未中,则停止投篮.同学甲投篮命中率为
,且每次投篮互不影响.
(Ⅰ)求同学甲恰好投4次达标的概率;
(Ⅱ)设同学甲投篮次数为X,求X的分布列.
| 2 | 3 |
(Ⅰ)求同学甲恰好投4次达标的概率;
(Ⅱ)设同学甲投篮次数为X,求X的分布列.
分析:(Ⅰ)同学甲恰好投4次测试达标,说明前3次有一次未投中,第4次必然投中,由独立重复试验的概率计算公式列式求解;
(Ⅱ)同学甲投篮次数最少为3次,包括达标和不达标,可以是4次,包括达标和不达标,最多是5次,也包括达标和不达标,由独立重复试验的概率计算出概率后列频率分布表.
(Ⅱ)同学甲投篮次数最少为3次,包括达标和不达标,可以是4次,包括达标和不达标,最多是5次,也包括达标和不达标,由独立重复试验的概率计算出概率后列频率分布表.
解答:解:(Ⅰ)同学甲恰好投4次测试达标,说明前3次有一次未投中,
所以同学甲恰好投4次达标的概率为P=
(
)(
)3=
;
(Ⅱ)X的取值为3,4,5
P(X=3)=(
)3+(
)3=
P(X=4)=
(
)(
)3+
(
)(
)3=
P(X=5)=
(
)2(
)2=
.
X的分布列
所以同学甲恰好投4次达标的概率为P=
| C | 1 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| 8 |
| 27 |
(Ⅱ)X的取值为3,4,5
P(X=3)=(
| 2 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
P(X=4)=
| C | 1 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| C | 1 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 10 |
| 27 |
P(X=5)=
| C | 2 4 |
| 1 |
| 3 |
| 2 |
| 3 |
| 8 |
| 27 |
X的分布列
| X | 3 | 4 | 5 | ||||||
| P |
|
|
|
点评:本题考查了离散型随机变量的分布列,考查了独立重复试验的概率计算公式,关键是读懂题意,计算出概率,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,
, ,求
,求 。
。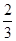 ,
,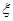 ,求
,求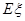 。
。