题目内容
14.现有语文书第一二三册,数学书第一二三册共六本书排在书架上,语文第一册不排在两端,数学书恰有两本相邻的排列方案种数( )| A. | 144 | B. | 288 | C. | 216 | D. | 360 |
分析 根据题意,分2种情况讨论:1、若语文第一册排在3本数学书之间,分3步进行分析:①、将三本数学书分为1-2的两组,将两组全排列,②、将语文第一册安排在数学书的两组之间,③、将3本数学书和语文第一册看成一个整体,与语文第二、三册全排列,2、若语文第一册不排在三本数学书之间,也需要分3步进行分析:①、安排语文第二、三册,将其全排列即可,②、安排3本数学书,先将将三本数学书分为1-2的两组,再在语文书的3个空位中,任选2个,安排2组数学书,③、安排语文第一册,分别求出每一步的情况数目,由分类计数原理计算可得答案.
解答 解:根据题意,分2种情况讨论:
1、若语文第一册排在3本数学书之间,分3步进行分析:
①、将三本数学书分为1-2的两组,有C31=3种分组方法,考虑2本一组的顺序,有2种情况,
将两组全排列,有A22=2种顺序,
②、将语文第一册安排在数学书的两组之间,有1种情况,
③、将3本数学书和语文第一册看成一个整体,与语文第二、三册全排列,有A33=6种情况,
此时不同的排法有3×2×2×6=72种排法;
2、若语文第一册不排在三本数学书之间,分3步进行分析:
①、将语文第二、三册全排列,有A22=2种顺序,排好后有3个空位可用,
②、将三本数学书分为1-2的两组,有C31=3种分组方法,
考虑2本一组的顺序,有2种情况,
在3个空位中,任选2个,安排2组数学书,有A32=6种情况,
则数学书的安排有3×2×6=36种情况,
③、数学书和2本语文书排好后,除去2端,有3个空位可选,
在3个空位中,任选1个,安排语文第一册,有C31=3种情况,
此时不同的排列方法有2×36×3=216种;
综合可得:不同的排列方法有72+216=288种;
故选:B.
点评 本题考查排列、组合的综合应用,关键是分析题意,确定分步分析的步骤.

 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
| A. | 命题“若a>1,则a2>1”的否命题为:“若a>1,则a2≤1” | |
| B. | 命题“?x0>1,使得-x02+2x0-1≥0”的否定“?x≤1,使得-x2+2x-1<0” | |
| C. | “x>-1”是“$\frac{1}{x}<-1$”成立的必要不充分条件 | |
| D. | 正弦函数是奇函数,f(x)=sin(x2+1)是正弦函数,所以f(x)=sin(x2+1)是奇函数,上述推理错误的原因是大前提不正确 |
| A. | 锐角三角形 | B. | 钝角三角形 | C. | 直角三角形 | D. | 等腰三角形 |
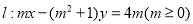 和圆
和圆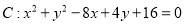 .有以下几个结论:
.有以下几个结论: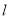 的倾斜角不是钝角;
的倾斜角不是钝角;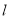 必过第一、三、四象限;
必过第一、三、四象限;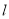 能将圆
能将圆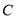 分割成弧长的比值为
分割成弧长的比值为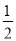 的两段圆弧;
的两段圆弧;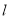 与圆
与圆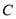 相交的最大弦长为
相交的最大弦长为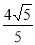 .
. 下边程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”,执行该程序框图时,若输入a,b分别为18,27,则输出的a=( )
下边程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”,执行该程序框图时,若输入a,b分别为18,27,则输出的a=( )