题目内容
椭圆M: 长轴上的两个顶点A、B,点P为椭圆M上除A、B外的一个动点,若
长轴上的两个顶点A、B,点P为椭圆M上除A、B外的一个动点,若 •
• =0且
=0且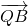 •
• =0,则动点Q在下列哪种曲线上
=0,则动点Q在下列哪种曲线上
- A.圆
- B.椭圆
- C.双曲线
- D.抛物线
B
分析:根据椭圆方程算出A(-a,0),B(A,0).设P(m,n),Q(x,y),可得 、
、 关于m、n、x、y的坐标形式,由
关于m、n、x、y的坐标形式,由 •
• =0建立关系式,化简得m+a=-
=0建立关系式,化简得m+a=- ,同理由
,同理由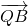 •
• =0建立关系式,得m-a=-
=0建立关系式,得m-a=- ,再将所得的两个式子对应相乘,结合点P(m,n)是椭圆
,再将所得的两个式子对应相乘,结合点P(m,n)是椭圆 上的点,化简得
上的点,化简得 ,即为动点Q的轨迹方程,可得本题答案.
,即为动点Q的轨迹方程,可得本题答案.
解答: 解:设P(m,n),Q(x,y)
解:设P(m,n),Q(x,y)
∵椭圆M的方程为 ,
,
∴作出椭圆如图所示,可得长轴的端点为A(-a,0),B(A,0)
∴ =(x+a,y),
=(x+a,y), =(m+a,n)
=(m+a,n)
∵ •
• =0,∴(x+a)(m+a)+ny=0,可得m+a=-
=0,∴(x+a)(m+a)+ny=0,可得m+a=- …①
…①
同理根据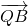 •
• =0,可得m-a=-
=0,可得m-a=- …②
…②
①×②,可得m2-a2= .…③
.…③
∵点P(m,n)是椭圆 上的动点,
上的动点,
∴ ,整理得n2=
,整理得n2= (a2-m2),
(a2-m2),
代入③可得:m2-a2= (a2-m2)•
(a2-m2)• ,化简得
,化简得
此方程对应的图形是焦点在y轴上的椭圆,可得动点Q的轨迹是一个椭圆,B项是正确答案
故选:B
点评:本题给出椭圆的长轴为AB,椭圆上的动点P满足若 •
• =0且
=0且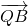 •
• =0,求动点Q的轨迹方程,着重考查了椭圆的简单几何性质、向量数量积的计算公式和动点轨迹方程的求法等知识,属于中档题.
=0,求动点Q的轨迹方程,着重考查了椭圆的简单几何性质、向量数量积的计算公式和动点轨迹方程的求法等知识,属于中档题.
分析:根据椭圆方程算出A(-a,0),B(A,0).设P(m,n),Q(x,y),可得
 、
、 关于m、n、x、y的坐标形式,由
关于m、n、x、y的坐标形式,由 •
• =0建立关系式,化简得m+a=-
=0建立关系式,化简得m+a=- ,同理由
,同理由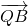 •
• =0建立关系式,得m-a=-
=0建立关系式,得m-a=- ,再将所得的两个式子对应相乘,结合点P(m,n)是椭圆
,再将所得的两个式子对应相乘,结合点P(m,n)是椭圆 上的点,化简得
上的点,化简得 ,即为动点Q的轨迹方程,可得本题答案.
,即为动点Q的轨迹方程,可得本题答案.解答:
 解:设P(m,n),Q(x,y)
解:设P(m,n),Q(x,y)∵椭圆M的方程为
 ,
,∴作出椭圆如图所示,可得长轴的端点为A(-a,0),B(A,0)
∴
 =(x+a,y),
=(x+a,y), =(m+a,n)
=(m+a,n)∵
 •
• =0,∴(x+a)(m+a)+ny=0,可得m+a=-
=0,∴(x+a)(m+a)+ny=0,可得m+a=- …①
…①同理根据
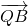 •
• =0,可得m-a=-
=0,可得m-a=- …②
…②①×②,可得m2-a2=
 .…③
.…③∵点P(m,n)是椭圆
 上的动点,
上的动点,∴
 ,整理得n2=
,整理得n2= (a2-m2),
(a2-m2),代入③可得:m2-a2=
 (a2-m2)•
(a2-m2)• ,化简得
,化简得
此方程对应的图形是焦点在y轴上的椭圆,可得动点Q的轨迹是一个椭圆,B项是正确答案
故选:B
点评:本题给出椭圆的长轴为AB,椭圆上的动点P满足若
 •
• =0且
=0且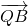 •
• =0,求动点Q的轨迹方程,着重考查了椭圆的简单几何性质、向量数量积的计算公式和动点轨迹方程的求法等知识,属于中档题.
=0,求动点Q的轨迹方程,着重考查了椭圆的简单几何性质、向量数量积的计算公式和动点轨迹方程的求法等知识,属于中档题. 
练习册系列答案
相关题目
 长轴上的两个顶点为
长轴上的两个顶点为 、
、 ,点P为椭圆M上除
,点P为椭圆M上除 ·
· =0,
=0, ·
· =0,则动点Q在下列哪种曲线上( )
=0,则动点Q在下列哪种曲线上( )