题目内容
已知椭圆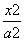
＋
＝1(a＞b＞0)的离心率为
，短轴的一个端点为M(0,1)．过椭圆左顶点A的直线l与椭圆的另一个交点为B.
(1)若
l与直线x＝a交于点P，求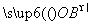
·
的值；
(2)若|AB|＝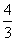
，求直线l的倾斜角．
解：(1)由题意知：
＝，b＝1.
又a2＝b2＋c2，
∴a＝
，
∴椭圆的方程为
＋y2＝1.
∵l过椭圆的左顶点A(－，0)，
∴设直线l：y＝k(x＋)．
∵直线x＝a，即为x＝，∴P(，2k)．
由
得(1＋2k2)x2＋4k2x＋4k2－2＝0.
可知x1＝－为此方程的一个根，设B(x2，y2)，
(2)∵|AB|＝
·|x1－x2|＝·|－－
|＝
，∴＝，
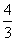化简得8k4－k2－7＝0，即(k2－1)(8k2＋7)＝0，
∴k2＝1或k2＝－
(舍去)，∴k＝±1，
∴直线l的倾斜角为
练习册系列答案
相关题目
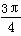，直线l1经过点A(3,2)、B(a，－1)，且l1与l垂直，直线l2：2x
＋by＋1＝0与直线l1平行，则a＋
－
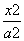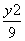＝1(a>0
)的
渐近线方程为3x±2y＝0，则a的值为( )
＝2
.
C的离心率；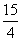
，求椭圆C的方程．
1
－
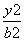＝1(a＞0，b＞0)的离心率为2.若抛物线C2：x2＝2py(p＞0)的焦点到双曲线C1的渐近线的距离为2，则抛物线C2的方程为( )
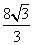y B．x2＝
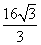y
(a＞0)，且满足条件sinC－sinB＝
sinA，则动点A的轨迹方程是________．