题目内容
求经过两圆(x+3)2+y2=13和x2+(y+3)2=37的交点,且圆心在直线x-y-4=0上的圆的方程.
剖析：根据已知,可通过解方程组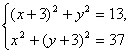
得圆上两点,
由圆心在直线x-y-4=0上,三个独立条件,用待定系数法求出圆的方程.
也可根据已知,设所求圆的方程为(x+3)2+y2-13+λ［x2+(y+3)2-37］=0,再由圆心在直线x-y-4=0上,定出参数λ,得圆方程.
解：因为所求的圆经过两圆(x+3)2+y2=13和x2+(y+3)2=37的交点,
所以设所求圆的方程为(x+3)2+y2-13+λ［x2+(y+3)2-37］=0.
展开、配方、整理,得(x+
)2+(y+
)2=
+
.
圆心为(-
,-
),代入方程x-y-4=0,得λ=-7.
故所求圆的方程为(x+
)2+(y+
)2=
.
讲评：圆C1:x2+y2+D1x+E1y+F1=0,圆C2:x2+y2+D2x+E2y+F2=0,若圆C1、C2相交,那么过两圆公共点的圆系方程为(x2+y2+D1x+E1y+F1)+λ(x2+y2+D2x+E2y+F2)=0(λ∈R且λ≠-1).它表示除圆C2以外的所有经过两圆C1、C2公共点的圆.
练习册系列答案
同步练习强化拓展系列答案
相关题目