题目内容
【题目】某校从参加高一年级期末考试的学生中抽出60名学生，将其数学成绩（均为整数）分成六段
， 
…
后，画出如下部分频率分布直方图.观察图形的信息，回答下列问题：
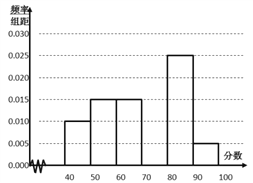
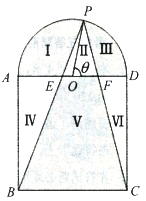
（1）求第四小组的频率，补全频率分布直方图，并估计该校学生的数学成绩的中位数.
（2）从被抽取的数学成绩是
分以上（包括
分）的学生中选两人，求他们在同一分数段的概率.
（3）假设从全市参加高一年级期末考试的学生中，任意抽取
个学生，设这四个学生中数学成绩为80分以上（包括
分）的人数为
（以该校学生的成绩的频率估计概率），求
的分布列和数学期望.
【答案】（1）
分.（2）
.（3）见解析.
【解析】试题分析：⑴通过各组的频率和等于
，求出第四组的频率，考查直方图，求出中位数即可； 
分别求出
， 
， 
的人数是
， 
， 
，然后利用古典概型概率求解即可；⑶判断概率类型
，即可写出
的分布列和数学期望
解析：（1）因为各组的频率和等于1，故第四组的频率：
.
直方图如图所示.
中位数是
，
估计这次考试的中位数是
分.
（2）
， 
， 
的人数是
， 
， 
，所以从成绩是
分以上（包括
分）的学生中选两人，他们在同一分数段的概率：
.
（3）因为
， 
， 
，
所以其分布列为：
| 0 | 1 | 2 | 3 | 4 |
| 0.2401 | 0.4116 | 0.2646 | 0.0756 | 0.0081 |
数学期望为
.
练习册系列答案
相关题目
