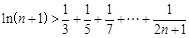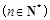题目内容
已知函数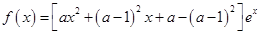 (其中
(其中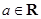 ).
).
(Ⅰ)若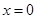 为
为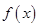 的极值点,求
的极值点,求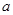 的值;
的值;
(Ⅱ)在(Ⅰ)的条件下,解不等式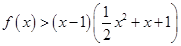 ;
;
(Ⅲ)若函数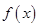 在区间
在区间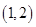 上单调递增,求实数
上单调递增,求实数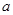 的取值范围.
的取值范围.
(1)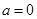 ;(2)
;(2)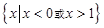 ;(3)
;(3)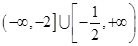 .
.
解析试题分析:本题考查导数的运算,利用导数研究函数的单调性、极值、最值、不等式等基础知识,考查函数思想、分类讨论思想,考查综合分析和解决问题的能力.第一问,因为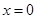 为
为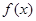 的极值点,所以
的极值点,所以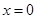 是
是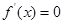 的根,所以对
的根,所以对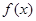 求导,解方程求出
求导,解方程求出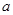 的值,最后检验一次
的值,最后检验一次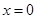 是不是
是不是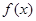 的极值点;第二问,先将不等式进行恒等变形,变成
的极值点;第二问,先将不等式进行恒等变形,变成 ,转化为不等式组,而对于
,转化为不等式组,而对于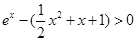 来说,式子比较复杂,不可以直接解不等式,那就构造新函数
来说,式子比较复杂,不可以直接解不等式,那就构造新函数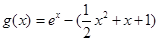 ,通过二次求导,判断函数的单调性,通过函数图像,数形结合解不等式;第三问,因为
,通过二次求导,判断函数的单调性,通过函数图像,数形结合解不等式;第三问,因为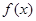 在
在 上单调递增,所以
上单调递增,所以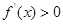 在
在 上恒成立,对
上恒成立,对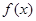 求导,由于
求导,由于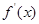 中含参数
中含参数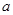 ,所以对
,所以对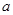 进行讨论,求出
进行讨论,求出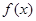 的增区间,利用
的增区间,利用 与增区间之间的子集关系,求参数
与增区间之间的子集关系,求参数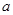 的取值范围.
的取值范围.
试题解析:(Ⅰ)因为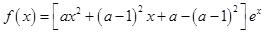
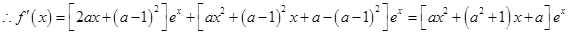 2分
2分
因为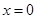 为
为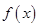 的极值点,所以由
的极值点,所以由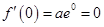 ,解得
,解得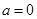 3分
3分
检验,当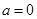 时,
时,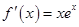 ,当
,当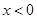 时,
时,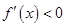 ,当
,当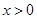 时,
时,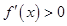 .
.
所以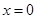 为
为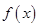 的极值点,故
的极值点,故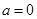 . 4分
. 4分
(Ⅱ) 当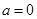 时,不等式
时,不等式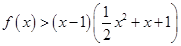
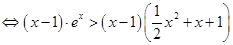 ,
,
整理得 ,即
,即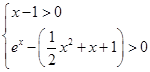 或
或 6分
6分
令 ,
,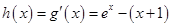 ,
,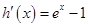 ,
,
当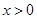 时,
时,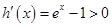 ;当
;当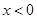 时,
时,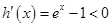 ,
,
所以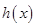 在
在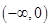 单调递减,在
单调递减,在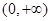 单调递增,所以
单调递增,所以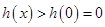 ,即
,即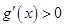 ,
,
所以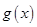 在
在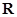 上单调递增,而
上单调递增,而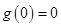 ;
;
故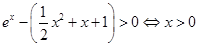 ;
; ,
,
所以原不等式的解集为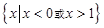 ; 8分
; 8分
(Ⅲ) 当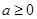 时,
时,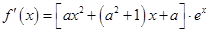
因为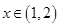 ,所以
,所以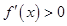 ,所以
,所以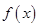 在
在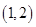 上是增函数.
上是增函数.
当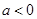 时,
时,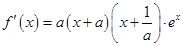 ,
, 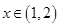 时,
时,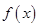 是增函数,
是增函数,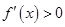 .
.
①若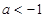 ,则
,则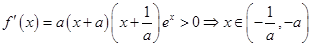 ,由
,由

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
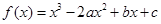 .
.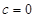 时,
时,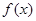 的图象在点
的图象在点 处的切线平行于直线
处的切线平行于直线 ,求
,求 的值;
的值;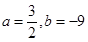 时,
时,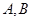 处有极值,
处有极值, 为坐标原点,若
为坐标原点,若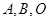 三点共线,求
三点共线,求 的值.
的值. ,其中
,其中 .
. ,求
,求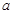 的值,并求此时曲线
的值,并求此时曲线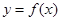 在点
在点 处的切线方程;
处的切线方程;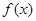 在区间
在区间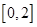 上的最小值.
上的最小值.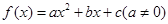 ,曲线
,曲线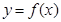 通过点(0,2a+3),且在
通过点(0,2a+3),且在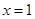 处的切线垂直于y轴.
处的切线垂直于y轴.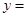 g(x)为偶函数,且当
g(x)为偶函数,且当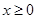 时,
时,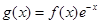 ,求当
,求当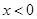 时g(x)的表达式,并求函数g(x)在R上的最小值及相应的x值.
时g(x)的表达式,并求函数g(x)在R上的最小值及相应的x值.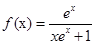 .
.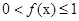 ;
;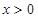 时,
时,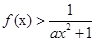 ,求
,求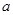 的取值范围.
的取值范围. ,
, .
. 恒成立,求实数
恒成立,求实数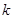 的值;
的值; 有一根为
有一根为 ,方程
,方程 的根为
的根为 ,是否存在实数
,是否存在实数 ?若存在,求出所有满足条件的
?若存在,求出所有满足条件的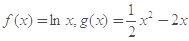 .
.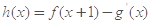 (其中
(其中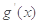 是
是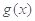 的导函数),求
的导函数),求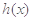 的最大值;
的最大值;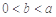 时,有
时,有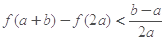 ;
;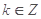 ,当
,当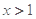 时,不等式
时,不等式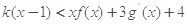 恒成立,求
恒成立,求 的最大值.
的最大值.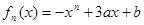 (
(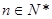 ,
,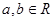 )。
)。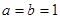 ,求
,求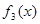 在
在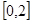 上的最大值和最小值;
上的最大值和最小值;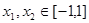 ,都有
,都有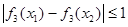 ,求
,求 的取值范围;
的取值范围;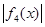 在
在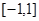 上的最大值为
上的最大值为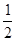 ,求
,求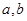 的值。
的值。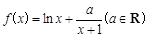 .
.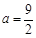 时,如果函数
时,如果函数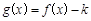 仅有一个零点,求实数
仅有一个零点,求实数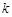 的取值范围;
的取值范围;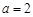 时,试比较
时,试比较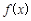 与1的大小;
与1的大小;