题目内容
函数y=sin(ωx+φ) 在区间
在区间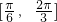 上单调递减,且函数值从1减小到-1,那么此函数图象与y轴交点的纵坐标为
上单调递减,且函数值从1减小到-1,那么此函数图象与y轴交点的纵坐标为
- A.

- B.

- C.

- D.
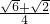
A
分析:依题意,利用正弦函数的单调性可求得y=sin(ωx+φ)的解析式,从而可求得此函数图象与y轴交点的纵坐标.
解答:∵函数y=sin(ωx+φ)在区间[ ,
, ]上单调递减,且函数值从1减小到-1,
]上单调递减,且函数值从1减小到-1,
∴ =
= -
- =
= ,
,
∴T=π,又T= ,
,
∴ω=2,
又sin(2× +φ)=1,
+φ)=1,
∴ +φ=2kπ+
+φ=2kπ+ ,k∈Z.
,k∈Z.
∴φ=2kπ+ ,k∈Z.
,k∈Z.
∵|φ|< ,
,
∴φ= .
.
∴y=sin(2x+ ),
),
令x=0,有y=sin =
= .
.
∴此函数图象与y轴交点的纵坐标为 .
.
故选A.
点评:本题考查由y=Asin(ωx+φ)的部分图象确定其解析式,求得ω与φ的值是关键,也是难点,考查分析与理解应用的能力,属于中档题.
分析:依题意,利用正弦函数的单调性可求得y=sin(ωx+φ)的解析式,从而可求得此函数图象与y轴交点的纵坐标.
解答:∵函数y=sin(ωx+φ)在区间[
 ,
, ]上单调递减,且函数值从1减小到-1,
]上单调递减,且函数值从1减小到-1,∴
 =
= -
- =
= ,
,∴T=π,又T=
 ,
,∴ω=2,
又sin(2×
 +φ)=1,
+φ)=1,∴
 +φ=2kπ+
+φ=2kπ+ ,k∈Z.
,k∈Z.∴φ=2kπ+
 ,k∈Z.
,k∈Z.∵|φ|<
 ,
,∴φ=
 .
.∴y=sin(2x+
 ),
),令x=0,有y=sin
 =
= .
.∴此函数图象与y轴交点的纵坐标为
 .
.故选A.
点评:本题考查由y=Asin(ωx+φ)的部分图象确定其解析式,求得ω与φ的值是关键,也是难点,考查分析与理解应用的能力,属于中档题.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
 设ω>0,函数y=sin(ωx+φ)(-π<φ<π)的图象向左平移
设ω>0,函数y=sin(ωx+φ)(-π<φ<π)的图象向左平移| π |
| 3 |
A、ω=1,?=
| ||
B、ω=2,?=
| ||
C、ω=1,?=-
| ||
D、ω=2,?=-
|
设ω>0,函数y=sin(ωx+
)的图象向右平移
个单位后与原图象重合,则ω的最小值是( )
| π |
| 3 |
| 4π |
| 3 |
A、
| ||
B、
| ||
| C、3 | ||
D、
|
 (2012•淄博一模)已知函数y=sin(ωx+φ)(ω>0,0<φ≤
(2012•淄博一模)已知函数y=sin(ωx+φ)(ω>0,0<φ≤