题目内容
 (2009•枣庄一模)如图,曲线C1:
(2009•枣庄一模)如图,曲线C1:| x2 |
| a2 |
| y2 |
| b2 |
(I)k1•k2是否与p无关?若是,给出证明;若否,给以说明;
(Ⅱ)若l2与y轴的交点为D(0,-2),当a2+b2取得最小值9时,求曲线C1与抛物线C2的方程.
分析:(I)求导函数,分别求出k1和k2,计算k1•k2,可得k1•k2仅与a,b有关,与p无关;
(II)先确定A的坐标,代入曲线C1的方程,利用基本不等式,结合a2+b2取得最小值9,即可求曲线C1与抛物线C2的方程.
(II)先确定A的坐标,代入曲线C1的方程,利用基本不等式,结合a2+b2取得最小值9,即可求曲线C1与抛物线C2的方程.
解答: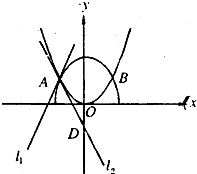 解:(I)设A(x0,y0),由
解:(I)设A(x0,y0),由
+
=1(b>a>0,y≥0)
得y=
,y′=-
,
则k1=y′|x=x0=-
…(2分)
由x2=2py(p>0)得y=
,则k2=y′|x=x0=
,
所以k1k2=-
•
=-
,(※) …(4分)
又因为
=2py0,y0=
,
则
=
,即
=
.
代入(※)式得k1k2=-
=-
•
=-2(
)2.
可见,k1•k2仅与a,b有关,与p无关. …(6分)
(II)如图,设A(x0,
),则x0∈(-a,0)
由(I)知k2=
,则l2:y=
(x-x0)+
.…(7分)
又l2过点D(0,-2),则
=4p,即x0=-2
,
所以A(-2
,2)…(8分)
将点A的坐标代入曲线C1的方程得
+
=1.
则a2+b2=(a2+b2)(
+
)=4p+4+
+
≥4p+4+8
,…(10分)
当且仅当“=”成立时,有
…(11分)
解得
所以C1:
+
=1(y≥0),C2:x2=
.…(14分)
 解:(I)设A(x0,y0),由
解:(I)设A(x0,y0),由| x2 |
| a2 |
| y2 |
| b2 |
得y=
| b |
| a |
| a2-x2 |
| bx | ||
a
|
则k1=y′|x=x0=-
| bx0 | ||||
a
|
由x2=2py(p>0)得y=
| x2 |
| 2p |
| x0 |
| p |
所以k1k2=-
| bx0 | ||||
a
|
| x0 |
| p |
b
| ||||
pa
|
又因为
| x | 2 0 |
| b |
| a |
a2-
|
则
| ||
| 2p |
b
| ||||
| a |
| ||||
|
| 2pb |
| a |
代入(※)式得k1k2=-
b
| ||||
pa
|
| b |
| pa |
| 2pb |
| a |
| b |
| a |
可见,k1•k2仅与a,b有关,与p无关. …(6分)
(II)如图,设A(x0,
| ||
| 2p |
由(I)知k2=
| x0 |
| p |
| x0 |
| p |
| ||
| 2p |
又l2过点D(0,-2),则
| x | 2 0 |
| p |
所以A(-2
| p |
将点A的坐标代入曲线C1的方程得
| 4p |
| a2 |
| 4 |
| b2 |
则a2+b2=(a2+b2)(
| 4p |
| a2 |
| 4 |
| b2 |
| 4a2 |
| b2 |
| 4pb2 |
| a2 |
| p |
当且仅当“=”成立时,有
|
解得
|
| x2 |
| 3 |
| y2 |
| 6 |
| y |
| 2 |
点评:本题考查曲线方程,考查直线与曲线的位置关系,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
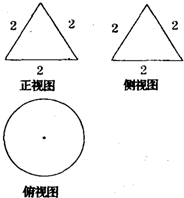 (2009•枣庄一模)一个几何体的三视图如图所示,则该几何体外接球的表面积为( )
(2009•枣庄一模)一个几何体的三视图如图所示,则该几何体外接球的表面积为( )