题目内容
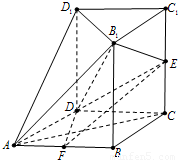
如图，几何体ABCDE中，△ABC是正三角形，EA和DC都垂直于平面ABC，且EA=AB=2a， DC=a，F、G分别为EB和AB的中点.
（1）求证：FD∥平面ABC；
（2）求证：AF⊥BD；
(3) 求二面角B—FC—G的正切值.
（Ⅰ）证明见解析（Ⅱ）证明见解析（Ⅲ）
解析:
证：(1)∵F、G分别为EB、AB的中点，
∴FG=
EA，又EA、DC都垂直于面ABC, FG=DC，
∴四边形FGCD为平行四边形，∴FD∥GC，又GC
面ABC，
∴FD∥面ABC.
（2）∵AB=EA，且F为EB中点，∴AF⊥EB ① 又FG∥EA，EA⊥面ABC
∴FG⊥面ABC ∵G为等边△ABC，AB边的中点，∴AG⊥GC.
∴AF⊥GC又FD∥GC，∴AF⊥FD ②
由①、②知AF⊥面EBD，又BD面EBD，∴AF⊥BD.
（3）由（1）、（2）知FG⊥GB，GC⊥GB，∴GB⊥面GCF.
过G作GH⊥FC，垂足为H，连HB，∴HB⊥FC.
∴∠GHB为二面角B-FC-G的平面角.
易求
.
练习册系列答案
相关题目
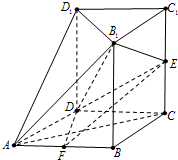（2013•青岛一模）如图，几何体ABCD-A1B1C1D1中，四边形ABCD为菱形，∠BAD=60°，AB=a，面B1C1D1∥面ABCD，BB1、CC1、DD1都垂直于面ABCD，且
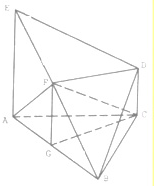如图，几何体ABCD中，△ABC是正三角形，EA和DC都垂直于平面ABC，且EA=AB=2a，DC=a，F、G分别为EB何AB的中点．
（2013•青岛一模）如图，几何体ABCD-B1C1D1中，四边形ABCD为菱形，∠BAD=60°，AB=a，面B1C1D1∥面ABCD，BB1、CC1、DD1都垂直于面ABCD，且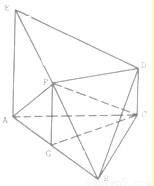
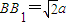，E为CC1的中点，F为AB的中点．