Question

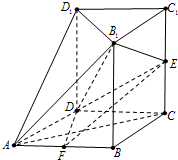（2013•青岛一模）如图，几何体ABCD-A₁B₁C₁D₁中，四边形ABCD为菱形，∠BAD=60°，AB=a，面B₁C₁D₁∥面ABCD，BB₁、CC₁、DD₁都垂直于面ABCD，且BB1=

2

a，E为CC₁的中点，F为AB的中点．
（Ⅰ）求证：△DB₁E为等腰直角三角形；
（Ⅱ）求二面角B₁-DE-F的余弦值．

Answer 1

分析：（Ⅰ）由已知条件，在直角三角形DBB₁，B₁C₁E，DCE中分别求出DB₁，B₁E，DE的长度，由边的关系能够证出
△DB₁E为等腰直角三角形；
（Ⅱ）取DB₁的中点H，因为O，H分别为DB，DB₁的中点，所以OH∥BB₁，以OA，OB，OH分别为x，y，z轴建立坐标系，求出两个平面DB₁E和DFE的法向量，根据二面角与其法向量所成角的关系求二面角B₁-DE-F的余弦值．

解答：（I）证明：连接BD，交AC于O，因为四边形ABCD为菱形，∠BAD=60°，所以BD=a
因为BB₁、CC₁都垂直于面ABCD，∴BB₁∥CC₁，又面B₁C₁D₁∥面ABCD，∴BC∥B₁C₁
所以四边形BCC₁B₁为平行四边形，则B₁C₁=BC=a
因为BB₁、CC₁、DD₁都垂直于面ABCD，则DB1=

DB2+BB12

=

a2+2a2

=

3

aDE=

DC2+CE2

=

a2+ a2 2

=

6 a

2

，B1E=

B1C12+C1E2

=

a2+ a2 2

=

6 a

2

所以DE2+B1E2=

6a2+6a2

4

=3a2=DB12
所以△DB₁E为等腰直角三角形；        
（II）解：取DB₁的中点H，因为O，H分别为DB，DB₁的中点，所以OH∥BB₁
以OA，OB，OH分别为x，y，z轴建立坐标系，
则D(0，-

a

2

，0)，E(-

3

2

a，0，

2

2

a)，B1(0，

a

2

，

2

a)，F(

3

4

a，

a

4

，0)
所以

DB1

=(0，a，

2

a)，

DE

=(-

3

2

a，

a

2

，

2

2

a)，

DF

=(

3

4

a，

3

4

a，0)
设面DB₁E的法向量为

n1

=(x1，y1，z1)，
则

n1

•

DB1

=0，

n1

•

DE

=0，即ay1+

2

az1=0且-

3

2

ax1+

a

2

y1+

2

2

az1=0
令z₁=1，则

n1

=(0，-

2

，1)
设面DFE的法向量为

n2

=(x2，y2，z2)，
则

n2

•

DF

=0，

n2

•

DE

=0即

3

4

ax2+

3

4

ay2=0且-

3

2

ax2+

a

2

y2+

2

2

az2=0
令x₂=1，则

n2

=(1，-

3

3

，

2 6

3

)
则cos＜

n1

，

n2

＞=

n1 • n2

| n1 || n2 |

=

6 3 + 2 6 3

3 × 1+ 1 3 + 8 3

=

2

2

，则二面角B₁-DE-F的余弦值为

2

2

．

点评：本题考查了三角形形状的判定，考查了二面角的平面角的求法，训练了平面法向量的求法，利用两个平面的法向量所成的角求解二面角时，要注意二面角和法向量所成角的关系，此题是中档题．