题目内容
已知f(x)+2f( )=2x+
)=2x+ (x≠0)
(x≠0)
(1)求f(x)的解析式;
(2)解关于x的不等式:3xf(x)<(k+4)x2-(k+1)x+2(其中k<0).
解:(1)∵f(x)+2f( )=2x+
)=2x+ (x≠0),
(x≠0),
∴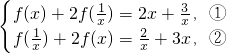 ,
,
①-②×2得3f(x)=4x+ ,
,
∴f(x)=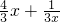 ,x≠0.
,x≠0.
(2)∵f(x)=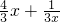 ,
,
3xf(x)<(k+4)x2-(k+1)x+2,k<0
∴kx2-(k+1)x+1>0,
即(kx-1)(x-1)>0,
∵k<0,
∴x∈( )∪(0,1).
)∪(0,1).
分析:(1)由f(x)+2f( )=2x+
)=2x+ (x≠0),知
(x≠0),知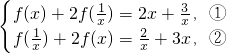 ,由此能求出f(x).
,由此能求出f(x).
(2)由f(x)=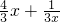 ,3xf(x)<(k+4)x2-(k+1)x+2,知kx2-(k+1)x+1>0,由此能求出关于x的不等式:3xf(x)<(k+4)x2-(k+1)x+2(其中k<0)的解集.
,3xf(x)<(k+4)x2-(k+1)x+2,知kx2-(k+1)x+1>0,由此能求出关于x的不等式:3xf(x)<(k+4)x2-(k+1)x+2(其中k<0)的解集.
点评:本题考查函数的解析式的求法,考查不等式的求解,是基础题.解题时要认真审题,仔细解答.
 )=2x+
)=2x+ (x≠0),
(x≠0),∴
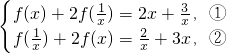 ,
,①-②×2得3f(x)=4x+
 ,
,∴f(x)=
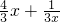 ,x≠0.
,x≠0.(2)∵f(x)=
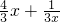 ,
,3xf(x)<(k+4)x2-(k+1)x+2,k<0
∴kx2-(k+1)x+1>0,
即(kx-1)(x-1)>0,
∵k<0,
∴x∈(
 )∪(0,1).
)∪(0,1).分析:(1)由f(x)+2f(
 )=2x+
)=2x+ (x≠0),知
(x≠0),知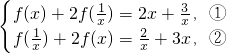 ,由此能求出f(x).
,由此能求出f(x).(2)由f(x)=
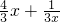 ,3xf(x)<(k+4)x2-(k+1)x+2,知kx2-(k+1)x+1>0,由此能求出关于x的不等式:3xf(x)<(k+4)x2-(k+1)x+2(其中k<0)的解集.
,3xf(x)<(k+4)x2-(k+1)x+2,知kx2-(k+1)x+1>0,由此能求出关于x的不等式:3xf(x)<(k+4)x2-(k+1)x+2(其中k<0)的解集.点评:本题考查函数的解析式的求法,考查不等式的求解,是基础题.解题时要认真审题,仔细解答.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目