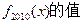题目内容
(本题满分15分)
已知函数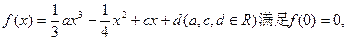
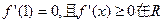 上恒成立.
上恒成立.
(1)求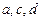 的值;
的值;
(2)若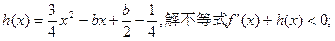
(3)是否存在实数m,使函数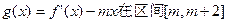 上有最小值-5?若存在,请求出实数m的值;若不存在,请说明理由.
上有最小值-5?若存在,请求出实数m的值;若不存在,请说明理由.
已知函数
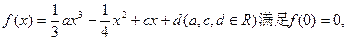
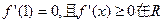 上恒成立.
上恒成立.(1)求
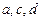 的值;
的值;(2)若
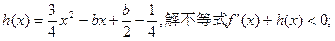
(3)是否存在实数m,使函数
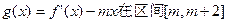 上有最小值-5?若存在,请求出实数m的值;若不存在,请说明理由.
上有最小值-5?若存在,请求出实数m的值;若不存在,请说明理由.(1)
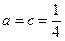 ;
;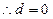
(2)当
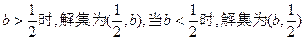
当
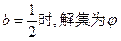
(3)
当
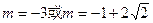 时,函数
时,函数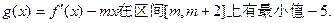
(1)
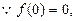
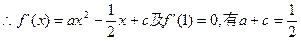
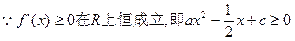 恒成立
恒成立即
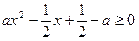 恒成立……………………2分
恒成立……………………2分显然
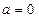 时,上式不能恒成立
时,上式不能恒成立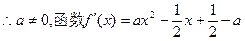 是二次函数
是二次函数由于对一切
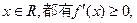 于是由二次函数的性质可得
于是由二次函数的性质可得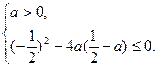
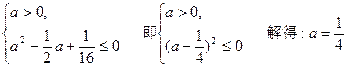
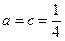 ………………………………4分
………………………………4分(2)
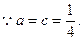
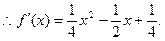
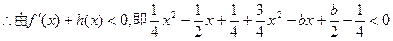
即
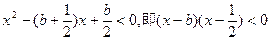 ………………6分
………………6分当
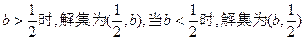
当
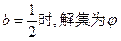 ……………………………………8分
……………………………………8分(3)
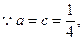
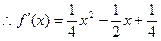
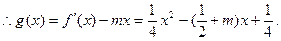
该函数图象开口向上,且对称轴为
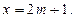
假设存在实数m
使函数
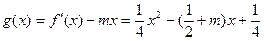 区间
区间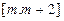 上有最小值-5.
上有最小值-5.①当
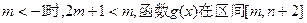 上是递增的.
上是递增的.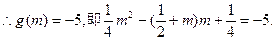
解得
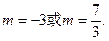
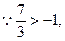
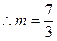 舍去.………………10分
舍去.………………10分②当
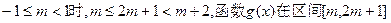 上是递减的,
上是递减的,而在区间
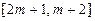 上是递增的,
上是递增的,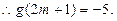
即
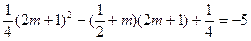
解得
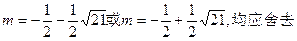 ………………12分
………………12分③当
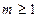 时,
时,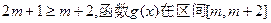 上递减的
上递减的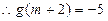
即
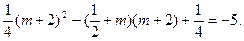
解得
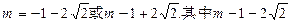 应舍去.
应舍去.综上可得,当
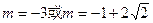 时,
时,函数
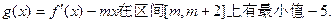 ………………15分
………………15分
练习册系列答案
 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
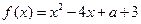 ,
,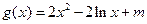
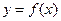 在[-1,1]上存在零点,求实数
在[-1,1]上存在零点,求实数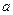 的取值范围;
的取值范围;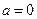 时,若对任意的
时,若对任意的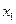 ∈[1,4],总存在
∈[1,4],总存在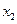 ∈[1,4],使
∈[1,4],使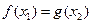 成立,求实数
成立,求实数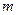 的取值范围;
的取值范围;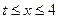 )的值域为区间D,是否存在常数
)的值域为区间D,是否存在常数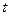 ,使区间D的长度为
,使区间D的长度为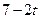 ?若存在,求出
?若存在,求出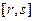 的长度为
的长度为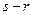 ).
).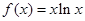 ,若
,若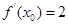 ,则 x 0 = ( *** )
,则 x 0 = ( *** )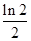

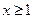 时, 证明: 不等式
时, 证明: 不等式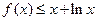 恒成立;
恒成立; 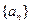 满足
满足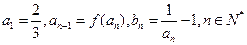 ,证明数列
,证明数列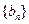 是等比数列,并求出数列
是等比数列,并求出数列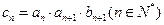 ,证明:
,证明: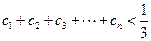 .
.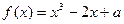 为奇函数,则其图象在点
为奇函数,则其图象在点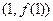 处的切线方程为__________。
处的切线方程为__________。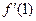 ="2" , 则a的值为 ( )
="2" , 则a的值为 ( ) 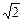

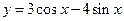 的导数为 .
的导数为 .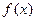 的导函数为
的导函数为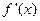 ,且满足
,且满足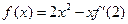 ,则
,则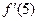 = .
= .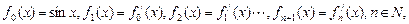 则
则