题目内容
12.已知α是第三象限角.f(α)=$\frac{sin(π-α)cos(2π-α)tan(-α+\frac{3π}{2})}{cos(-α-π)}$.(1)若cos(α-$\frac{3π}{2}$)=$\frac{1}{5}$,求f(α)的值;
(2)若α=-1920°,求f(α)的值.
分析 (1)由已知条件利用诱导公式求出sinα=-$\frac{1}{5}$,f(a)=cosα,再由α是第三象限角,利用同角三角函数关系式能求出结果.
(2)由α=-1920°,f(a)=cosα,利用诱导公式能求出结果.
解答 解:(1)∵cos(α-$\frac{3π}{2}$)=$\frac{1}{5}$,∴sinα=-$\frac{1}{5}$,
∵α是第三象限角,
∴f(a)=$\frac{sin(π-α)cos(2π-α)tan(-α+\frac{3π}{2})}{cos(-α-π)}$
=$\frac{sinα(-cosα)cotα}{-cosα}$
=cosα
=-$\sqrt{1-(-\frac{1}{5})^{2}}$
=-$\frac{2\sqrt{6}}{5}$.
(2)∵α=-1920°=-$\frac{32π}{3}$,
∴f(a)=$\frac{sin(π-α)cos(2π-α)tan(-α+\frac{3π}{2})}{cos(-α-π)}$
=cosα
=cos(-$\frac{32π}{3}$)=cos$\frac{32π}{3}$
=cos$\frac{2π}{3}$
=-cos$\frac{π}{3}$
=-$\frac{1}{2}$.
点评 本题考查三角函数值的求法,是中档题,解题要认真审题,注意诱导公式和同角三角函数关系式的合理运用.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
17.已知函数f(x)=x3+bx2+cx+d的图象如图所示,则函数y=log${\;}_{\frac{1}{2}}$(x2+$\frac{2}{3}$bx+$\frac{c}{3}$)的单调减区间为( )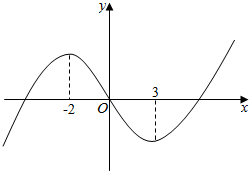

| A. | ($\frac{1}{2}$,+∞) | B. | (3,+∞) | C. | (-∞,-$\frac{1}{2}$) | D. | (-∞,-2) |
9.设P和Q是两个集合,定义集合P+Q={x|x∈P}或x∈Q且x∉P∩Q.若P={x|x2-5x-6≤0},Q={x|y=log2(x2-2x-15)},那么P+Q等于( )
| A. | [-1,6] | B. | (-∞,-1]∪[6,+∞) | C. | (-3,5) | D. | (-∞,-3)∪[-1,5]∪(6,+∞) |
 如图所示,有一个堤坝,原斜坡AB长50m,坡角∠ABC=40°,现要将斜坡的坡角改成25°,即∠D=25°,那么斜坡的坡底要延长多少(精确到0.1m)?
如图所示,有一个堤坝,原斜坡AB长50m,坡角∠ABC=40°,现要将斜坡的坡角改成25°,即∠D=25°,那么斜坡的坡底要延长多少(精确到0.1m)?